Question

Find the tension.

Answer 1

As a first step, you could make a free body diagram marking all the forces acting the block. Then you could balance the forces acting in the vertical direction from the fact that there is no vertical motion. After that you could balance the forces in the horizontal directions along the plane and thus get the tension.
Formula used:
Frictional force,
$f=\mu N$

Complete step by step answer:
In the question, we are given a block of 1kg that is kept on an inclined plane of inclination$37{}^\circ$. The coefficient friction between the block and the plane is given to be 0.8. We are supposed to find the tension in the string attached to the block.
As a first step, let us make the free body diagram of the given block marking all the forces acting on it. Since, there is a value for coefficient of friction, we should understand there is a frictional force on the block.

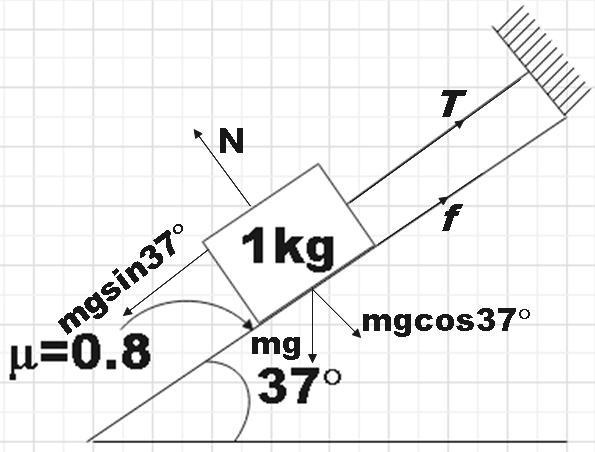
Since, there is no vertical motion for the block, we could say that,
$N=mg\cos 37{}^\circ$
Now, we have the frictional force on the block which can be given by,
$f=\mu N$
$\Rightarrow f=0.8\times mg\cos 37{}^\circ =0.8\times 1\times 10\times 0.798=6.39N$ ………………………… (1)
Now, we could balance the forces in the horizontal direction along the inclined plane.
$T+f=mg\sin 37{}^\circ$
$\Rightarrow T=\left( 1\times 10\times 0.6 \right)-f=6-6.4$
$\therefore T=-0.4N$
Therefore, we found the tension in the string to be -0.4N. The negative value for tension indicated that the direction of the tension in the string would be opposite to that assigned in the figure.

Note: One should be very careful while making a free body diagram as missing out any one of the forces acting on the block would make your answer incorrect. Also, direction of these forces is also important. Here, we have simply resolved the weight of the block mg into its components. And the direction of the frictional force is marked by the fact that it will oppose the possible motion.