Solveeit Logo
Login

Question

Question: Find the sum of final charges on \({C_2}\) and \({C_3}\) if a capacitor \({C_1} = 1.0\mu F\) is char...

Find the sum of final charges on C2{C_2} and C3{C_3} if a capacitor C1=1.0μF{C_1} = 1.0\mu F is charged up to a voltage V=60VV = 60V by connecting it to a battery BB through switch (1) and now, C1{C_1} is disconnected from a battery and connected to a circuit consisting of two uncharged capacitors C2=3.0μF{C_2} = 3.0\mu F and C3=6.0μF{C_3} = 6.0\mu F through a switch (2) as shown in the figure.

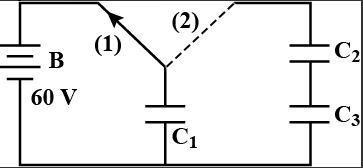
A. 40μC40\mu C
B. 36μC36\mu C
C. 20μC20\mu C
D. 54μC54\mu C

Explanation

Solution

Hint First of all, calculate the equivalent capacitance between C2{C_2} and C3{C_3}. Then, calculate the charge passing from C1{C_1} by using the formula of charge, Q=CVQ = CV (where, QQ is the charge, CC is the capacitance and VV is the potential difference across the capacitor).
Next, evaluate the potential difference between equivalent capacitors and C1{C_1}.
Then, calculate the charge across the equivalent capacitance.

Complete step-by-step solution :Let C′C' be the equivalent capacitance of C2{C_2} and C3{C_3}.
As shown in figure, C2{C_2} and C3{C_3} are in series so, to calculate equivalent resistance, we have to use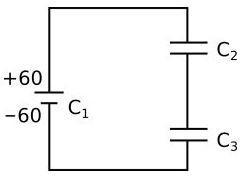

1C′=1C2+1C3 ⇒1C′=C2+C3C2C3 ∴C′=C2C3C2+C3  \dfrac{1}{{C'}} = \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} \\\ \Rightarrow \dfrac{1}{{C'}} = \dfrac{{{C_2} + {C_3}}}{{{C_2}{C_3}}} \\\ \therefore C' = \dfrac{{{C_2}{C_3}}}{{{C_2} + {C_3}}} \\\
Now, putting the values of C2{C_2} and C3{C_3} in the above expression –
C′=3×63+6 C′=189=2μF  C' = \dfrac{{3 \times 6}}{{3 + 6}} \\\ C' = \dfrac{{18}}{9} = 2\mu F \\\
Now, calculating the charge across the capacitor, C1=1.0μF{C_1} = 1.0\mu F
∵Q=CV\because Q = CV
According to the question, the capacitance, C1{C_1} is charged up to a voltage V=60VV = 60V
∴Q1=1×60 Q1=60μC  \therefore {Q_1} = 1 \times 60 \\\ {Q_1} = 60\mu C \\\
The potential difference between C1{C_1} and C′C' combined.
V′=Q1C1+C′V' = \dfrac{{{Q_1}}}{{{C_1} + C'}}
Putting the values of capacitance and charge of C1{C_1} in the above expression –
V′=601+2 ⇒V′=603 ∴V′=20V  V' = \dfrac{{60}}{{1 + 2}} \\\ \Rightarrow V' = \dfrac{{60}}{3} \\\ \therefore V' = 20V \\\
Now, calculating the charge of C2{C_2} and C3{C_3} system –
Q23=C′V′{Q_{23}} = C'V'
Putting the values of C′C' and V′V' on the above expression –
Q23=2×20=40μC{Q_{23}} = 2 \times 20 = 40\mu C
Therefore, the charge on capacitors C2{C_2} and C3{C_3} is 40μC40\mu C.
Hence, option (A) is the correct answer.

Note:- The device which is used to store electrical energy is called a capacitor. The capacity of the capacitor to store the electricity is called Capacitance. The S.I unit of capacitance is Farad which is denoted by F.F.
The dimensional formula of capacitor is M−1L−2I2T4.{M^{ - 1}}{L^{ - 2}}{I^2}{T^4}.