Question

Find the solution set of the equation $\left( 2\cos x+1 \right)\left( 4\cos x+5 \right)=0$ in the interval $\left[ 0,2\pi \right]$.

Answer 1

Hint: Use zero product property. Use the fact that if $\cos x=\cos y$, then $x=2n\pi \pm y,n\in \mathbb{Z}$. Use the fact that $\forall x\in \left[ -1,1 \right],\cos \left( \arccos x \right)=x$. Hence find the general solutions of the given system and hence find the solutions in the interval $\left[ 0,2\pi \right]$. Verify the number of solutions graphically.

Complete Step-by-step answer:
We have $\left( 2\cos x+1 \right)\left( 4\cos x+5 \right)=0$
We know that if ab =0, then a = 0 or b = 0 (Zero product property).
Applying zero product property, we get
$2\cos x+1=0$ or $4\cos x+5=0$
Solving 2cosx+1 = 0:
Subtracting 1 from both sides, we get
$2\cos x=-1$
Dividing by 1 on both sides, we get
$\cos x=\dfrac{-1}{2}$
We know that $\cos \left( \arccos \left( \dfrac{-1}{2} \right) \right)=\dfrac{-1}{2}$.
We know $\arccos \left( -x \right)=\pi -\arccos x$
Hence we have
$\arccos \left( \dfrac{-1}{2} \right)=\pi -\arccos \left( \dfrac{1}{2} \right)=\pi -\dfrac{\pi }{3}=\dfrac{2\pi }{3}$
Hence the given equation becomes
$\cos x=\cos \left( \dfrac{2\pi }{3} \right)$
We know that if $\cos x=\cos y$, then $x=2n\pi \pm y,n\in \mathbb{Z}$
Hence we have
$x=2n\pi \pm \dfrac{2\pi }{3}$
Put n = 0, we get
$x=\dfrac{2\pi }{3},\dfrac{-2\pi }{3}$
Since in the interval $\left[ 0,2\pi \right]$, we have $x\ge 0$, we have $x=\dfrac{2\pi }{3}$
Put n = 1, we get
$x=\dfrac{4\pi }{3},\dfrac{8\pi }{3}$
Since in the interval $\left[ 0,2\pi \right]$, we have $x\le 2\pi$, we have $x=\dfrac{4\pi }{3}$
Hence the solutions are \left\\{ \dfrac{2\pi }{3},\dfrac{4\pi }{3} \right\\}
Solving 4cosx + 5 = 0:
Subtracting 5 from both sides, we get
$4\cos x=-5$
Dividing both sides by 4, we get
$\cos x=-\dfrac{5}{4}$
Now we know that $\forall x\in \mathbb{R},\cos x\in \left[ -1,1 \right]$ and since $-1\ge \dfrac{-5}{4}$, we have there exists no x such that $\cos x=\dfrac{-5}{4}$.
Hence the equation 4cosx+5 = 0 has no solutions.
Hence the solution set of the given equation is \left\\{ \dfrac{2\pi }{3},\dfrac{4\pi }{3} \right\\}.

Note: While solving a trigonometric equation, special care must be taken about the domain and the range of each function. In the solution above note that $\dfrac{-5}{4}$ was out of range and hence we removed it from our solution set. Trigonometric equations often lead to extraneous roots that have to be removed from the solution set. This process gets very easy if while solving, we take care of the domain and range of each function.
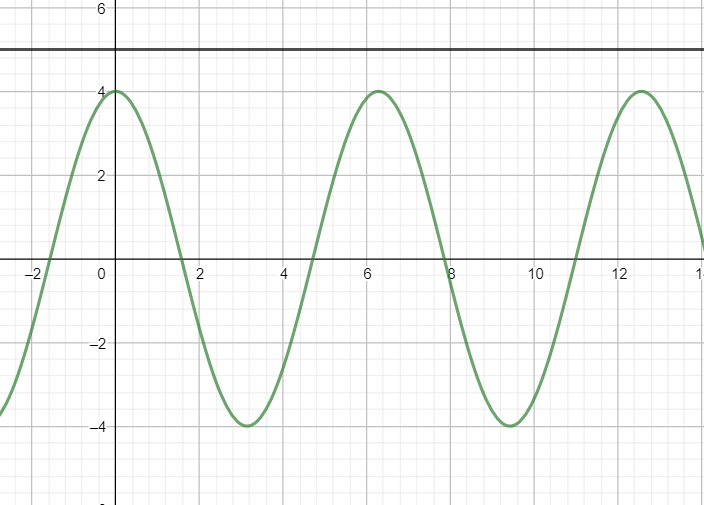
The plot of y = 4cosx and y = 5 is shown below. Notice that these graphs do not intersect each other.

The graph of y = 2cosx and y = 1 is shown below. Notice that in the interval $\left[ A=0,B=2\pi \right]$, they intersect at two points C and D.

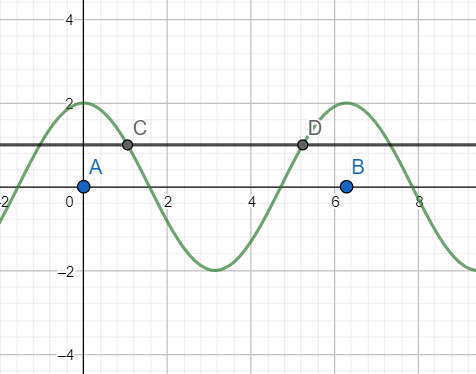
Hence our solution is correct.