Question

Find the solution for the bisector AG of triangle ABC in terms of vectors ‘a’ and ‘b’. Given that: G is the centroid of the triangle ABC if ${\text{AB = a}}$,${\text{AC = b}}$ respectively.
(a) ${\text{AG = }}\dfrac{{\bar a - \bar b}}{3}$
(b) ${\text{AG = }}\dfrac{{\bar a + \bar b}}{3}$
(c) ${\text{AG = }}\dfrac{{\bar a + \bar b}}{2}$
(d) None of the above

Answer 1

We will use the most curious concept of vector geometry which depends on both magnitude and direction of the problem, we are going to use the centroid formula in terms of vector definition and then substituting the values by solving the given conditions, the desired answer can be obtained.

Complete step-by-step solution:

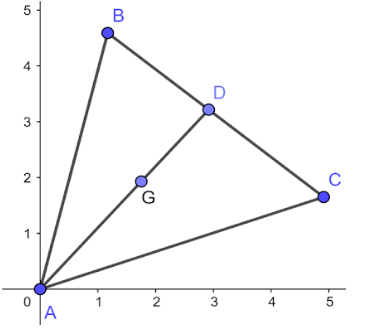
$\Rightarrow$ Figure implies that position vectors of ‘A’ is $\vec a$, ‘B’ is $\vec b$, ‘C' is $\vec c$.
Since, the problem implies the centroid condition which is the intersection of the median ‘AD’ at point ‘G’,
So, according to vector definition, we know the centroid formula
$\overrightarrow{G} = \dfrac{{\overrightarrow a + \overrightarrow b + \overrightarrow c }}{3}$… (i)
But, we have given that ‘AG’ is the bisector of the triangle ABC i.e. $\vartriangle {\text{ABC}}$
Hence, according to the centroid formula [equation (i)],
$\Rightarrow$Bisector$\overrightarrow {AG} {\text{ = }}\dfrac{{\overrightarrow a + \overrightarrow b + \overrightarrow c }}{3}$… (ii)
Where, the point ‘A’ is the origin of the vector $\vartriangle {\text{ABC}}$
$\therefore$The vector equation of the point ‘A’ is $A \equiv (0,0,0)$ i.e. $\overrightarrow a {\text{ = }}0$
The equation becomes (ii),
$\Rightarrow \overrightarrow {AG} {\text{ = }}\overrightarrow g {\text{ - }}\overrightarrow a {\text{ = }}\overrightarrow g {\text{ }} = {\text{ }}\dfrac{{\overrightarrow a + \overrightarrow b + \overrightarrow c }}{3}$
$\Rightarrow \overrightarrow {AG} {\text{ = }}\dfrac{{0 + \overrightarrow b + \overrightarrow c }}{3}$
Where, the position vectors of ‘B’ and ‘C’ are ‘$\vec a$’ and ‘$\vec b$’ respectively
(Refer the figure above),
Therefore, the equation becomes,
$\Rightarrow \overrightarrow {AG} {\text{ = }}\dfrac{{\overrightarrow a + \overrightarrow b }}{3}$
$\therefore \Rightarrow$T he option (b) is correct.

Note: Note that the notation used to express the vector condition can be shown either by ‘$\vec a$’ or $\bar a$both are same so no need to be confused in rest of the problems referred to in any other books, etc. Also one must know the definition of vector geometry and its rules to apply such as ‘for cross-product, dot-product, conditions for parallel and perpendicular vectors, triangle law of addition (used in this case) that is, etc. $AB{\text{ }} + {\text{ }}BC{\text{ }} = {\text{ }}AC$’ and also remember the centroid, midpoint formula in terms of vector geometry (since by adding the notation above the respective variable).