Question
Question: Find the slope of the line passing through the points: (i) (-2, 3) and (8, -5) (ii) (4, -3) and...
Find the slope of the line passing through the points:
(i) (-2, 3) and (8, -5)
(ii) (4, -3) and (6, -3)
(iii) (3, 2) and (3, -1)
Solution
Hint: We know that the slope of a line joining the two points (x1,y1) and (x2,y2) is equal to the tangent of the angle made by the line with x-axis in anticlockwise direction by as follows:
slope=tanθ=x2−x1y2−y1
Complete step-by-step answer:
We will find the slope of a line passing through the following points as below:
(i) (-2, 3) and (8, -5)
We know that the slope of a line passing through the two points (x1,y1) and (x2,y2) is given by,
slope=x2−x1y2−y1

So we have x1=−2,y1=3,x2=8,y2=−5
⇒slope=8−(−2)−5−3=8+2−8=10−8=5−4
Hence the slope is equal to (5−4).
(ii) (4, -3) and (6, -3)
We know that slope of a line passing through the points (x1,y1) and (x2,y2) is given by,
slope=x2−x1y2−y1
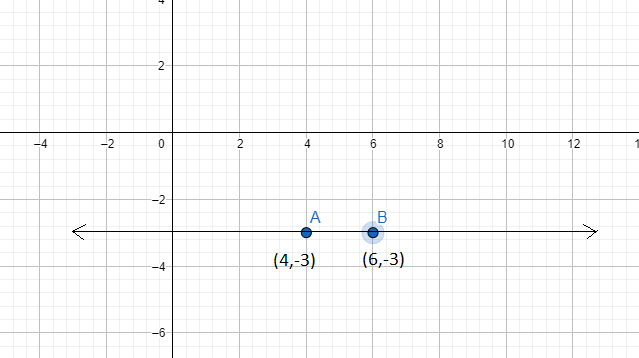
So we have x1=4,y1=−3,x2=6,y2=−3
⇒slope=6−4−3−(−3)=20=0
Since we know that if the slope of a line is equal to 0 means the line is parallel to x-axis.
Hence, slope is equal to zero.
(iii) (3, 2) and (3, -1)
We know that the slope of a line passing through the points (x1,y1) and (x2,y2) is given by,
slope=x2−x1y2−y1
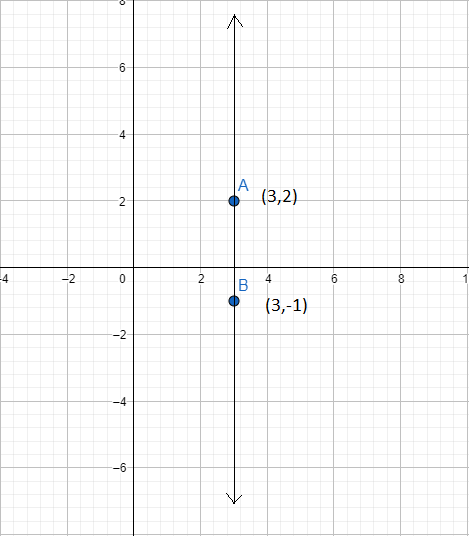
⇒slope=3−3−1−2=0−3=∞(infinity)
Hence the slope is equal to infinity means the line is perpendicular to the x-axis.
Note: Substitute the value of x1,y1,x2,y2 in the formula very carefully because if you misplace it order then you will get the incorrect answer. Also, remember that the slope of a line is also equal to the tangent value of the angle by the line and the x-axis in anticlockwise direction with respect to x-axis.
