Question

Find the shortest distance of the point (0,c) from the parabola $y={{x}^{2}}\text{ where 0}\le \text{c }\le \text{5}\text{.}$

Answer 1

- Hint: In the above question we will assume a variable point on the parabola and then we will use the method of derivative to minimize the variable distance between the given point and the variable point on the parabola. We will use the distance formula between two points which is as follows:
S = Distance between two points (a,b) and (c,d) = $\sqrt{{{(d-b)}^{2}}+{{(c-a)}^{2}}}$

**Complete step-by-step solution :**
Let us consider any point $(h,{{h}^{2}})$ on the parabola. The figure would be like:

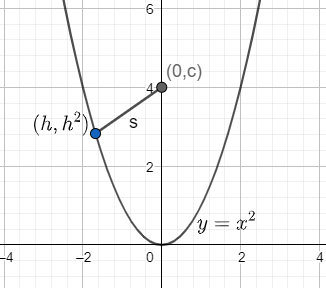
Distance of this point from (0,c),

& s=\sqrt{{{(h-0)}^{2}}+{{({{h}^{2}}-c)}^{2}}} \\\ & \Rightarrow {{s}^{2}}={{h}^{2}}+{{h}^{4}}+{{c}^{2}}-2{{h}^{2}}c \\\ & \Rightarrow {{s}^{2}}={{h}^{4}}+{{h}^{2}}(1-2c)+{{c}^{2}} \\\ \end{aligned}$$ $${{s}^{2}}$$ is the variable of which we need to find minima. We will find the first derivative with respect to h. $$\begin{aligned} & 2s\dfrac{ds}{dh}=4{{h}^{3}}+2h(1-2c)=0 \\\ & \Rightarrow h(4{{h}^{2}}+2(1-2c))=0 \\\ & \Rightarrow h=0\text{ or }h=\pm \sqrt{\dfrac{2c-1}{2}} \\\ \end{aligned}$$ When $$0 < c < \dfrac{1}{2}$$, we get a negative value for $${{h}^{2}}$$. Hence, h = 0 gives the shortest distance. In this case shortest distance = c. When $$c > \dfrac{1}{2}$$ , the first derivative changes sign from –ve to +ve at $$h=\pm \sqrt{\dfrac{2c-1}{2}}$$ . Hence, we get the minimum there. In this case, we have $$\begin{aligned} & s=\sqrt{{{h}^{4}}+{{h}^{2}}(1-2c)+{{c}^{2}}} \\\ & \Rightarrow \sqrt{{{\left( c-\dfrac{1}{2} \right)}^{2}}-2{{\left( c-\dfrac{1}{2} \right)}^{2}}+{{c}^{2}}} \\\ & \Rightarrow \sqrt{{{c}^{2}}-{{\left( c-\dfrac{1}{2} \right)}^{2}}} \\\ & \Rightarrow \sqrt{\dfrac{1}{2}\times \left( 2c-\dfrac{1}{2} \right)}=\dfrac{1}{2}\sqrt{4c-1} \\\ \end{aligned}$$ **Therefore, the shortest distance is “c” when $$0 < c < \dfrac{1}{2}$$ and the shortest distance is $$\dfrac{1}{2}\sqrt{4c-1}$$, when $$c > \dfrac{1}{2}$$.** **Note:** Just be careful while doing calculation because there is a chance that you will make a silly mistake and you will get. Also, remember the distance formula and the concept of derivative to find minima and maxima as it will help you a lot in these types of questions.