Question

Find the shortest distance of the point (0,c) from the parabola $y={{x}^{2}}$ where $0\le c\le 5$.
(a) $\sqrt{\dfrac{4c-1}{2}}$
(b) $\sqrt{\dfrac{4c-2}{4}}$
(c) $\sqrt{\dfrac{4c-3}{3}}$
(d) $\sqrt{\dfrac{4c-1}{4}}$

Answer 1

Draw the graph for the parabola $y={{x}^{2}}$ with vertex at (0,0) and draw a normal from P (0,c) to the parabola. This normal will be the shortest distance between the point and the parabola. The best approach is using calculus we can find the slope of Normal.

Complete step-by-step solution:
The parabola $y={{x}^{2}}$ is drawn below along with normal from P (0, c) to the parabola.

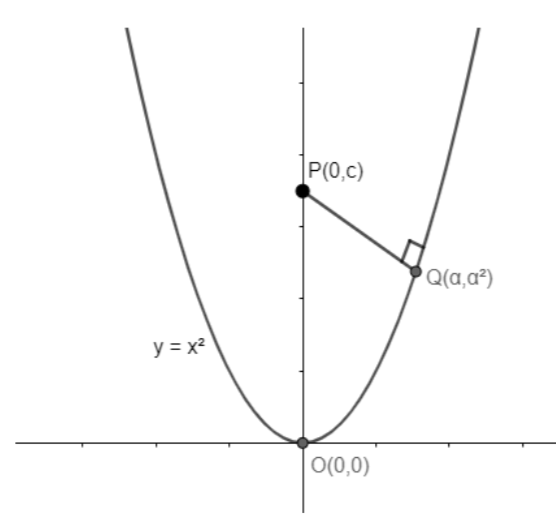
Let the normal intersect the parabola at $Q\left( \alpha ,{{\alpha }^{2}} \right)$. Hence, PQ will the shortest distance from point P to the parabola. We have to find the distance between point P and Q.
Finding the slope of normal drawn, we get,
$y={{x}^{2}}$
Differentiating both sides with respect to x, we get,
$\Rightarrow \dfrac{dy}{dx}=2x$
Now, at $\dfrac{dy}{dx}$ at Q will give the slope of tangent,
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{at\text{ }Q}}=2\alpha$
Since the tangent and normal are perpendicular to each other, i.e., ${{m}_{1}}{{m}_{2}}=-1$, hence, the slope of normal will be given by
${{m}_{1}}{{m}_{2}}=-1$
$\Rightarrow 2\alpha {{m}_{1}}=-1$
$\Rightarrow {{m}_{1}}=\dfrac{-1}{2\alpha }$
Slope of Normal, $m=-\dfrac{1}{2\alpha }...............(i)$
Also, since we have coordinates of two points P and Q, so using the formula of two – point form to find the slope of normal.
The two – point form is given by the equation $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}................(ii)$
From the given coordinates P (0, c) and $Q\left( \alpha ,{{\alpha }^{2}} \right)$, we have,
${{x}_{1}}=0,{{y}_{1}}=c$
${{x}_{2}}=\alpha ,{{y}_{2}}={{\alpha }^{2}}$
Now, replacing the values of ${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}}$ in equation (i), we get,
$m=\dfrac{{{\alpha }^{2}}-c}{\alpha -0}..............(iii)$
From equation (i) and (iii), we get,
$-\dfrac{1}{2\alpha }=\dfrac{{{\alpha }^{2}}-c}{\alpha -0}$
$\Rightarrow -\dfrac{1}{2\alpha }=\dfrac{{{\alpha }^{2}}-c}{\alpha }$
$\Rightarrow -\dfrac{1}{2}={{\alpha }^{2}}-c$
$\Rightarrow {{\alpha }^{2}}-c=-\dfrac{1}{2}$
$\Rightarrow {{\alpha }^{2}}=c-\dfrac{1}{2}$
$\Rightarrow \alpha =\pm \sqrt{c-\dfrac{1}{2}}$
Thus, the coordinates of point Q is $\left( \pm \sqrt{c-\dfrac{1}{2}},c-\dfrac{1}{2} \right)$.
We know, the distance between the two points is given by the formula:
$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}...............(iv)$
Using the formula (iv) to find the distance between the point PQ, we get,
${{x}_{1}}=0,{{y}_{1}}=c$
${{x}_{2}}=\pm \sqrt{c-\dfrac{1}{2}},{{y}_{2}}=c-\dfrac{1}{2}$
Now, replacing the values of ${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}}$ in equation (iv), we get,
$PQ=\sqrt{{{\left( 0\mp \sqrt{c-\dfrac{1}{2}} \right)}^{2}}+{{\left( c-\dfrac{1}{2}-c \right)}^{2}}}$
$\Rightarrow PQ=\sqrt{{{\left( \mp \sqrt{c-\dfrac{1}{2}} \right)}^{2}}+{{\left( c-c-\dfrac{1}{2} \right)}^{2}}}$
$\Rightarrow PQ=\sqrt{\left( c-\dfrac{1}{2} \right)+{{\left( -\dfrac{1}{2} \right)}^{2}}}$
$\Rightarrow PQ=\sqrt{c-\dfrac{1}{2}+\dfrac{1}{4}}$
$\Rightarrow PQ=\sqrt{c-\dfrac{1}{4}}$
$\therefore PQ=\sqrt{\dfrac{4c-1}{4}}$

Note: The best approach to solve this question is to make use of calculus. In order to find the shortest distance from a point to any geometric figure is to draw a normal from the point to the figure. Students must take care of the difference between the tangent and normal. There is a relation between the slopes of a tangent and normal, i.e., ${{m}_{1}}{{m}_{2}}=-1$.