Question

Find the set of values of $k$ for which the equation ${x^2} + 2\left( {k - 1} \right)x + k - 1 = 0$ has no real roots?

Answer 1

To find the set of values of $k$ for which the equation ${x^2} + 2\left( {k - 1} \right)x + k - 1 = 0$ has no real roots, we will use the concept of discriminant which is denoted by $D$. As, we know that for an equation $a{x^2} + bx + c = 0$ to have no real roots $D < 0$ i.e., ${b^2} - 4ac < 0$. We will put the values and solve the inequality to get the possible values.

Complete step by step answer:
We have been given a quadratic equation ${x^2} + 2\left( {k - 1} \right)x + k - 1 = 0$ and we have to find the value of $k$ for which the given equation has no real roots.
As we know that the given equation is of the form $a{x^2} + bx + c = 0$ and to have no real roots the value of discriminant of an equation must be less than zero i.e., $D < 0$.
Now, we know that $D = {b^2} - 4ac$
The given quadratic equation is ${x^2} + 2\left( {k - 1} \right)x + k - 1 = 0$. Here, $a = 1$, $b = 2\left( {k - 1} \right)$ and $c = k - 1$.
Putting all these values in the formula in $D < 0$, we get
$\Rightarrow {b^2} - 4ac < 0$
$\Rightarrow {\left[ {2(k - 1)} \right]^2} - 4 \times \left( 1 \right) \times \left( {k - 1} \right) < 0$
On simplification, we get
$\Rightarrow \left[ {4({k^2} - 2k + 1)} \right] - 4(k - 1) < 0$
Taking $4$ common, we get
$\Rightarrow 4\left( {{k^2} - 2k + 1 - k + 1} \right) < 0$
As we know, inequality remains the same when dividing both sides by a positive number.
Dividing both the sides by $4$, we get
$\Rightarrow {k^2} - 2k + 1 - k + 1 < 0$
On simplification, we get
$\Rightarrow {k^2} - 3k + 2 < 0$
On splitting the middle term, we get
$\Rightarrow {k^2} - k - 2k + 2 < 0$
Taking the terms common, we get
$\Rightarrow k\left( {k - 1} \right) - 2\left( {k - 1} \right) < 0$
Now taking $\left( {k - 1} \right)$ common, we get
$\Rightarrow \left( {k - 1} \right)\left( {k - 2} \right) < 0$
On solving this inequality, we get

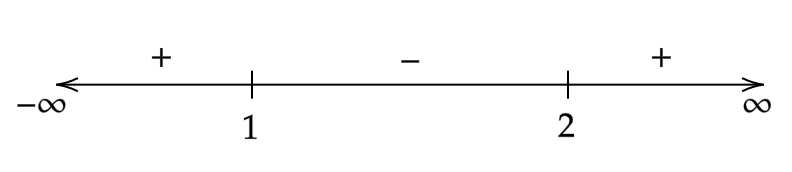
For $k > 2$, we get $\left( {k - 1} \right)\left( {k - 2} \right) > 0$.
For $1 < k < 2$, we get $\left( {k - 1} \right)\left( {k - 2} \right) < 0$.
For $k < 1$, we get $\left( {k - 1} \right)\left( {k - 2} \right) > 0$.
So, we get $\left( {k - 1} \right)\left( {k - 2} \right) < 0$ for $k \in \left( {1,2} \right)$.
Therefore, the set of values of $k$ for which the equation ${x^2} + 2\left( {k - 1} \right)x + k - 1 = 0$ has no real roots is $k \in \left( {1,2} \right)$.

Note: Here, $1$ and $2$ are not included in the set of values of $k$. Here, one point to note is that square bracket $\left[ {} \right]$ states that the end elements of the range will satisfy the given expression whereas the round bracket $\left( {} \right)$ states that the end elements will not satisfy the given expression.