Question

Find the set of values of a for which

$\frac{ax^2+2(a+1)x+9a+4}{-x^2+4x+5}>0$

Answer 1

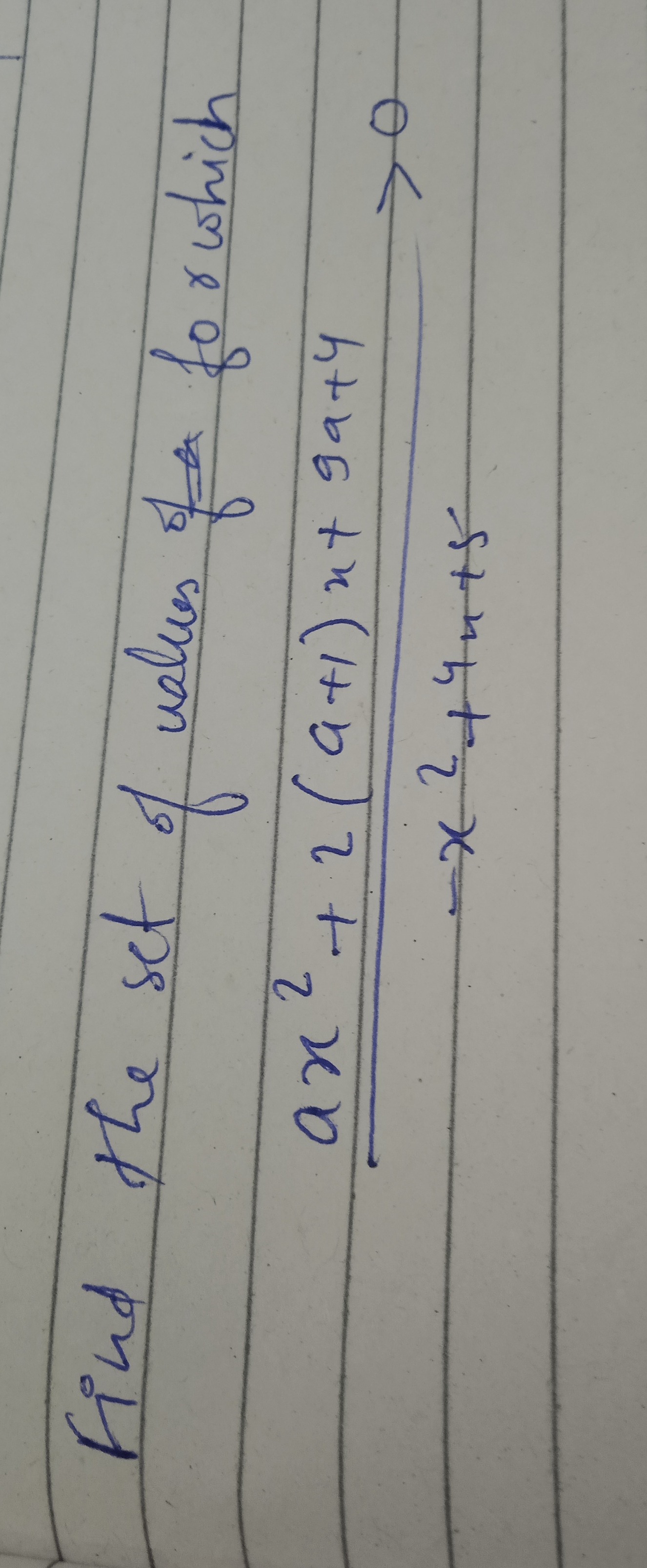
There is no real number $a$ such that

$$\frac{ax^2+2(a+1)x+9a+4}{-x^2+4x+5}>0\quad\text{for all real }x\text{ (with }-x^2+4x+5\ne 0\text{)}.$$

Answer 2

We wish to find all real numbers $a$ such that

$$\frac{ax^2+2(a+1)x+9a+4}{-x^2+4x+5}>0\quad\text{for all real }x\text{ (with }-x^2+4x+5\ne0\text{)}.$$

A typical strategy for “for all‑$x$” problems is to make sure that the numerator and the denominator have the same sign for every $x$ (except when the denominator is 0). Note that the denominator

$$D(x)=-x^2+4x+5$$

can be rewritten as

$$9-(x-2)^2.$$

Thus,

• $D(x)>0$ when $(x-2)^2<9$ i.e. when $-1<x<5,$
• $D(x)<0$ when $x<-1$ or $x>5$.

For the fraction to be positive for every $x$ (where it is defined) we must have

• In the interval $-1<x<5$ (where $D(x)>0$): the numerator $N(x)=ax^2+2(a+1)x+9a+4$ must be positive.
• In the regions $x<-1$ and $x>5$ (where $D(x)<0$): we must have $N(x)<0$ so that the ratio is positive.

Since $N(x)$ is a quadratic it can change its sign only once (i.e. it has at most two zeros). In fact, if its leading coefficient is negative (so that it is “∩‐shaped”), then it will be positive only between its two real roots and negative outside. Hence, for the sign of $N(x)$ to “mimic” that of $D(x)$ we would need the two zeros of $N(x)$ to occur exactly at the points where $D(x)=0$, namely at $x=-1$ and $x=5$. (If the zeros were different the sign–changes would not line up with the intervals where the denominator has a fixed sign.)

Thus we impose

$$N(-1)=0\quad \text{and}\quad N(5)=0.$$

Let’s compute these:

1. At $x=-1$:)

   $$N(-1)=a(-1)^2+2(a+1)(-1)+9a+4 = a -2(a+1)+9a+4.$$

   Simplify:

   $$=a-2a-2+9a+4=8a+2.$$

   Setting $N(-1)=0$ gives

   $$8a+2=0\quad\Longrightarrow\quad a=-\frac{1}{4}.$$

2. At $x=5$:)

   $$N(5)=a(25)+2(a+1)(5)+9a+4=25a+10a+10+9a+4.$$

   Simplify:

   $$=44a+14.$$

   Setting $N(5)=0$ gives

   $$44a+14=0\quad\Longrightarrow\quad a=-\frac{14}{44}=-\frac{7}{22}.$$

For the desired situation we would need both conditions to be satisfied simultaneously. However,

$$-\frac{1}{4}\approx -0.25\quad\text{and}\quad -\frac{7}{22}\approx -0.318,$$

and clearly

$$-\frac{1}{4}\ne -\frac{7}{22}.$$

Thus, it is impossible for the numerator to change sign exactly at $x=-1$ and $x=5$. In other words, there is no real number $a$ for which

$$\frac{ax^2+2(a+1)x+9a+4}{-x^2+4x+5}>0\quad\text{for all }x\text{ (with }-x^2+4x+5\ne0\text{)}.$$