Question
Question: Find the resultant of three vectors \(\overrightarrow{OA}\), \(\overrightarrow{OB}\) and \(\overrigh...
Find the resultant of three vectors OA, OB and OC shown in the figure given below. Radius of the circle is R.
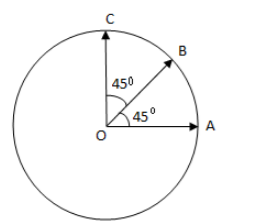
Solution
Vectors cannot be added simply as scalars are added because they have magnitude as well as direction. All the three vectors are in different directions. We will find their components in X direction and in Y direction.
Complete step by step answer:
Vector is a quantity which has both magnitude and direction. It is represented by an arrow whose direction is the same as that of the quantity and whose length is proportional to the quantity’s magnitude. A vector is not altered if it is displaced parallel to itself.
To add the given three vectors we will find their components in X direction and in Y direction.Let us take the direction of OA as X axis and perpendicular to this, which is the direction of OC as Y axis. Therefore, OA The vector is in X direction only and has no component in Y direction.OC has its component only in the Y direction.
Vector OB is making 45∘angle with the X axis as well as with the Y axis.
OA=OB=OC=R (given)
X components:-
Sum of vectors in x direction=vx
vx= Rcos0+Rcos45+Rcos90
⇒vx=R+2R+0
⇒vx=R(1+21)
Sum of y Components=
vx=Rsin90+Rsin45+Rsin0 ⇒vx=R+2R+0 ⇒vx=R(1+21)
⇒Resultant vector=vx2+vy2
⇒Resultant=[R(1+21)]2+[R(1+21)]2
⇒Resultant=R2(1+21)2
∴Resultant=R(2+1)
Hence, the resultant of three vectors is R(1+2).
Note: We can use the parallelogram law of vector addition first for two vectors and then using their resultant vector with the third vector to calculate the resultant of three vectors. Do not add the vectors simply and do not forget to find their components to get the resultant vector.
