Question

Find the resultant of the following forces.

Answer 1

These kind of questions to be solved by resolution of vectors. Every vector can be resolved into two components along the perpendicular axes. Here perpendicular axes are the x axis and the y axis. We have the angle made by the vector with x axis hence we can resolve the vector components along the x axis and finally add them to get net force along x axis and we will do the same along y- axis to get force component along y axis.

Complete step-by-step answer:

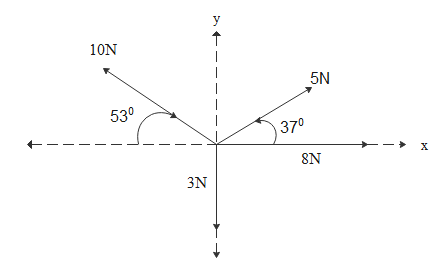
In the given question
5N vector is making ${37^0}$ with the x axis and 10N vector is making ${53^0}$ with the x axis and 8N vector is along the x axis
Now component of 10N vector along x axis is $10\cos ({53^0})$ in negative x axis direction
Let it be A = $- 10\cos ({53^0}) = - 10 \times \dfrac{3}{5} = - 6N$
Now component of 5N vector along x axis is $5\cos ({37^0})$ in positive x axis direction
Let it be B = $5\cos ({37^0}) = 5 \times \dfrac{4}{5} = 4N$
Now component of 8N vector along x axis is $8\cos ({0^0})$ in positive x axis direction
Let it be C = $8\cos ({0^0}) = 8 \times 1 = 8N$
Now adding all the components along x axis we get
$A + B + C = - 6 + 4 + 8 = 6N$
Coming to forces along y axis
5N vector is making ${37^0}$ with the x axis and 10N vector is making ${53^0}$ with the x axis and 3N vector is along the y axis
Now component of 10N vector along y axis is $10\sin ({53^0})$ in positive y axis direction
Let it be A = $10\sin ({53^0}) = 10 \times \dfrac{4}{5} = 8N$
Now component of 5N vector along y axis is $5\sin ({37^0})$ in positive y axis direction
Let it be B = $5\sin ({37^0}) = 5 \times \dfrac{3}{5} = 3N$
Now component of 3N vector along negative y axis is $3\cos ({0^0})$ in negative y axis direction
Let it be C = $- 3\cos ({0^0}) = - 3 \times 1 = - 3N$
Now adding all the components along y axis we get
$A + B + C = 8 + 3 - 3 = 8N$
Hence the resultant will be
$R = 6\mathop i\limits^ \wedge + 8\mathop j\limits^ \wedge$
Magnitude of resultant will be $\sqrt {{8^2} + {6^2}} = 10$

Note: Generally the angle we take with reference to x-axis must be taken in anti clock wise direction to get correct answer. Here in case of 10N we took in the clock wise direction and we compensated it later by multiplying that x component with negative sign. If angle is already taken anticlockwise then no need to multiply with a negative sign