Question

Find the resistance of a hollow cylindrical conductor of length 1m with inner radius 1.0 mm and outer radius 2.0 mm respectively. The resistivity of the material is $2.0 \times {10^{ - 8}}\Omega m$.
${\text{A}}{\text{. 2}}{\text{.1}} \times {\text{1}}{{\text{0}}^{ - 3}}\Omega \\\ {\text{B}}{\text{. 1}}{\text{.3}} \times {\text{1}}{{\text{0}}^{ - 4}}\Omega \\\ {\text{C}}{\text{. 3}}{\text{.2}} \times {\text{1}}{{\text{0}}^{ - 4}}\Omega \\\ {\text{D}}{\text{. 4}}{\text{.6}} \times {\text{1}}{{\text{0}}^{ - 2}}\Omega \\\$

Answer 1

The resistance of a material is equal to the product of the resistivity of the material and the ratio of length to the cross-sectional area of the conductor. We are given the value of length of the conductor and the resistivity of the material. We just need to find out the cross sectional area of the conductor from given information.

Formula used:
The resistance of a conductor is given as
$R = \rho \dfrac{l}{A}$
Here $\rho$ represents the resistivity of the material of the conductor while l is the length and A is the cross-sectional area of the given conductor.

Complete step by step answer:
We are given a hollow cylindrical conductor. Its length is given as
$l = 1m$
We are also given the inner and outer radius of this cylindrical conductor with inner radius 1.0 mm and outer radius 2.0 mm respectively. From this information, we can calculate the cross-sectional area of the conductor which is equal to the difference between surface area due to the outer radius and the surface area due to the inner radius.

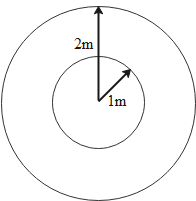
It is given as
$A = \pi {\left( 2 \right)^2} - \pi {\left( 1 \right)^2} = 4\pi - \pi = 3\pi = 3 \times 3.14 = 9.42m{m^2} \\\ = 9.42 \times {10^{ - 6}}{m^2} \\\$
We are also given the resistivity of the material of the conductor which is
$\rho = 2.0 \times {10^{ - 8}}\Omega m$
Now we can easily calculate the resistance of the given cylindrical conductor by using the formula for resistance which involves various parameters we have calculated above. The resistance of the conductor in terms of these parameters is given as
$R = \rho \dfrac{l}{A}$
Now substituting all the known values, we get
$R = \dfrac{{2.0 \times {{10}^{ - 8}} \times 1}}{{9.42 \times {{10}^{ - 6}}}} = 0.212 \times {10^{ - 2}}\Omega \\\ = 2.12 \times {10^{ - 3}}\Omega \\\$
This is the required answer and hence, the correct answer is option A.

Note:
1. Take care of the units of the quantities, they all should be in the same system of units.
2. The ratio of the length of the conductor to the cross-sectional area of the conductor is the quantity which actually decides the resistance of a conductor. This is because the resistivity of a given material is fixed irrespective of the dimensions of the conductor.