Question
Question: Find the relation between \({{m}_{1}}\), \({{m}_{2}}\) and \({{m}_{3}}\) so that \({{m}_{3}}\) remai...
Find the relation between m1, m2 and m3 so that m3 remains at rest. (Assume m1>m2)
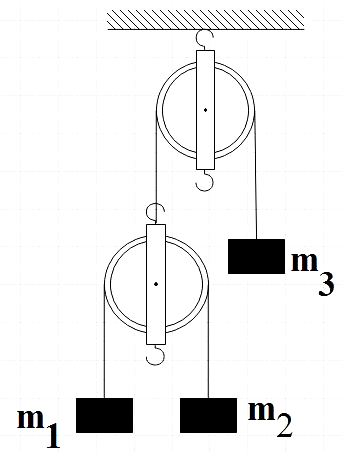
Solution
As a first step, mark all the forces (including tension in the string) acting on each of these masses and also find the net force on each mass. Also, find the net acceleration (a) of the whole system. As per the question net force on m3 is 0 (at rest). The equations for net force in the case of other two masses can be subtracted from each other accordingly and then substituting for ‘a’ and rearranging will lead you to the relation between the given three masses.
Formula used:
Newton’s second law,
F=ma
Complete step by step answer:
We are given the system with three masses m1, m2 and m3 as shown in the above figure. We are asked to find the relationship between these masses so that the third mass m3 is at rest.
Let us suppose that both the pulley and the string are very light and also the friction is absent everywhere. Keeping this in mind let us redraw the above figure showing all the forces acting on the system.
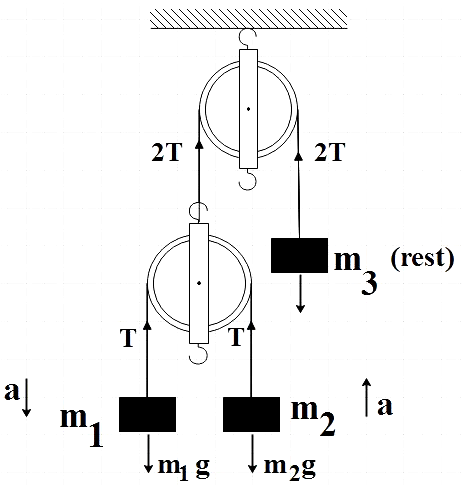
All that we have to do here is to find the net force acting each mass. Also, let us make an assumption that m1>m2 .
Firstly, let us consider mass m1:
There is tension acting in the upward direction along the string and also there is weight of the body acting downward due to gravitation. As a resultant of these two forces, the body is accelerated downward. So, the net force on the mass m1 is,
F1=m1g−T
By Newton’s second law, F=ma
m1g−T=m1a ………………………….. (1)
Now let us go for mass m2:
Just like the previous case there are two forces acting on the body – tension and weight, due which the body is accelerated. But here in this case, the body is accelerated in the opposite direction, that is, in downward direction. So, the net force on the mass m2 is,
F2=T−m2g
T−m2g=m2a …………………………… (2)
Now let us move on to the third mass m3. Since, we are given the question that m3is at rest, the tension acting along the string carrying the third mass should be 2T. Also, the net force acting on the body should be zero in order for it to be at rest.
F3=2T−m3g=0
2T=m3g ………………………… (3)
Net acceleration in the second pulley is given by the relation,
a=MFNET
a=m1+m2m1g−m2g …………………………… (4)
Subtracting (2) from (1) we get,
(m1+m2)g−2T=(m1−m2)a
Substituting (3) and (4) we get,
(m1+m2)g−m3g=(m1−m2)(m1+m2m1−m2g)……………………. (5)
Dividing (5) by g and multiplying the same with (m1+m2) on both sides we get,
(m1+m2)2−(m1−m2)2=m3(m1+m2)
LHS is in the form ofa2−b2 , but we know, a2−b2=(a+b)(a−b)
(2m1)(2m2)=m3(m1+m2)
By rearranging we get,
m34=m11+m21
Hence, the relation betweenm1,m2 and m3 so that m3remains at rest is given by,
m34=m11+m21
Note: While dealing with net force acting on a body, you should be aware of which direction the body will accelerate as the result of this net force. So that, you will know which force acting on the body is greater so as to cause the acceleration in that particular direction. A free-body diagram is a must while solving such problems.
