Question
Question: Find the regular Expression for the FA (Finite Automata) using Arden's Theorem. ...
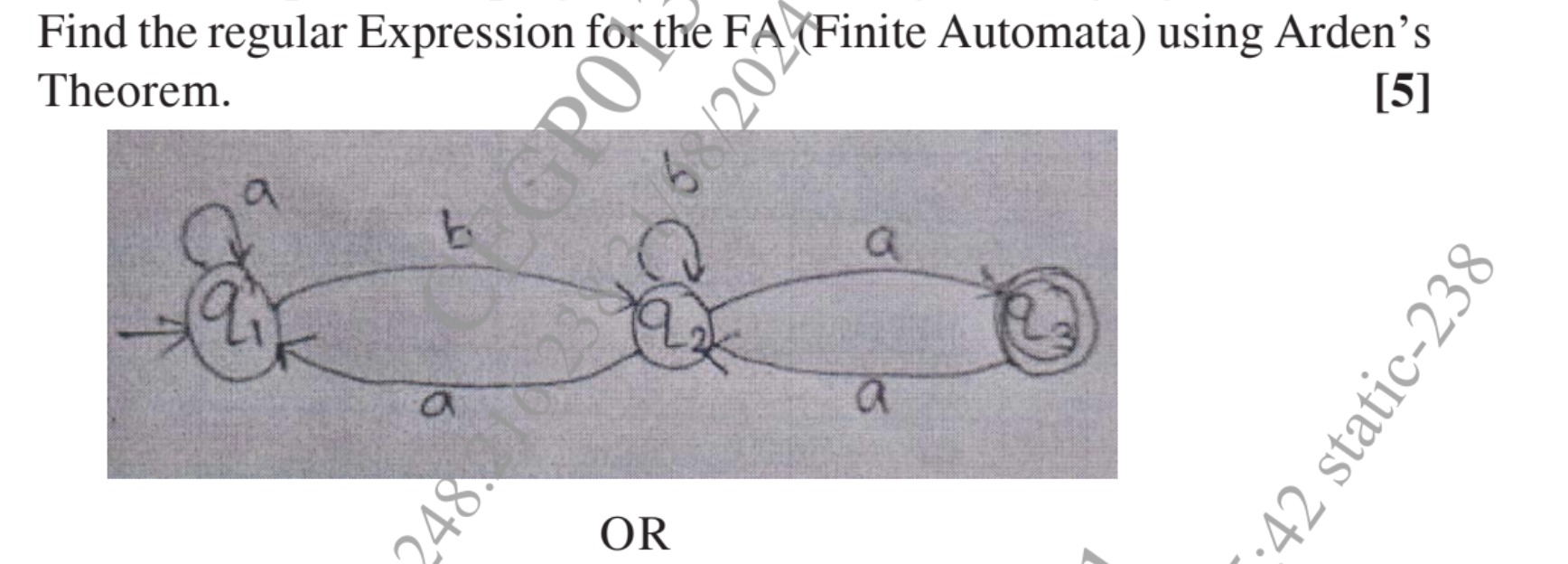
Find the regular Expression for the FA (Finite Automata) using Arden's Theorem.
R = (a + b(b + aa)a) b(b + aa)* a
Solution
To find the regular expression for the given Finite Automata (FA) using Arden's Theorem, we first write down the equations for each state.
1. Define States and Transitions: Let q1,q2,q3 be the regular expressions representing the set of all strings that can take the FA from the initial state to states q1,q2,q3 respectively.
- q1 is the initial state, so it has an ϵ transition.
- q3 is the final state.
2. Write Equations for Each State: Based on the transitions in the FA:
-
For state q1:
- It's the initial state, so it includes ϵ.
- There's a self-loop on q1 with 'a'.
- There's a transition from q2 to q1 with 'a'. Equation for q1: q1=ϵ+q1a+q2a (Equation 1)
-
For state q2:
- There's a transition from q1 to q2 with 'b'.
- There's a self-loop on q2 with 'b'.
- There's a transition from q3 to q2 with 'a'. Equation for q2: q2=q1b+q2b+q3a (Equation 2)
-
For state q3:
- There's a transition from q2 to q3 with 'a'. Equation for q3: q3=q2a (Equation 3)
3. Solve the Equations using Arden's Theorem: Arden's Theorem states that if an equation is of the form R=Q+RP, where Q and P are regular expressions and R does not contain R in Q, then the solution is R=QP∗.
Substitute Equation 3 into Equation 2: q2=q1b+q2b+(q2a)a q2=q1b+q2b+q2aa q2=q1b+q2(b+aa)
Now, apply Arden's Theorem to solve for q2. Here, R=q2, Q=q1b, and P=(b+aa). q2=q1b(b+aa)∗ (Equation 4)
Now substitute Equation 4 into Equation 1: q1=ϵ+q1a+(q1b(b+aa)∗)a q1=ϵ+q1a+q1b(b+aa)∗a q1=ϵ+q1(a+b(b+aa)∗a)
Apply Arden's Theorem to solve for q1. Here, R=q1, Q=ϵ, and P=(a+b(b+aa)∗a). q1=ϵ(a+b(b+aa)∗a)∗ Since ϵR=R, q1=(a+b(b+aa)∗a)∗ (Equation 5)
Finally, we need the regular expression for the language accepted by the FA, which is the expression for the final state q3. Substitute Equation 5 into Equation 4, and then the result into Equation 3:
Substitute q1 (Equation 5) into q2 (Equation 4): q2=(a+b(b+aa)∗a)∗b(b+aa)∗ (Equation 6)
Now, substitute q2 (Equation 6) into q3 (Equation 3): q3=q2a q3=((a+b(b+aa)∗a)∗b(b+aa)∗)a
This is the regular expression for the given FA.
Explanation of the solution:
- Define regular expressions for each state (q1,q2,q3) representing strings from the initial state to that state.
- Formulate a system of linear equations based on the FA's transitions. q1 is initial, so it gets ϵ.
- Solve the system of equations using Arden's Theorem (R=Q+RP⟹R=QP∗) by substituting equations backwards from the final state.
- The regular expression for the FA is the expression for the final state (q3).
