Question

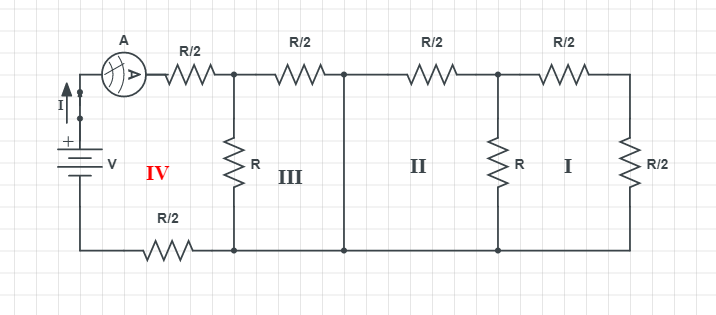
Find the reading of the ammeter in the circuit given below

$A.\dfrac{V}{2R}$
$B.\dfrac{3V}{4R}$
$C.\dfrac{2V}{7R}$
$D.\dfrac{11V}{R}$

Answer 1

We have to reduce the circuit to find the equivalent resistance. We must keep in mind that current always travels through the least resistance path. So at the junction of part three and two, current flows through the path with no resistance. Thus only part three and two of the circuit contributes to the equivalent resistance.

Formula used:
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}+.......$
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+..........$
$V=IR$

Complete step by step answer:
Let us reduce the given circuit to its equivalent circuit.
To reduce it let us divide the circuit diagram into four parts

Equivalent resistance when two or more resistors are connected in series
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}+.......$

When connected in parallel
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+..........$ $\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+..........$

The equivalent resistance in part one is

$\begin{aligned} & \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{\dfrac{R}{2}+\dfrac{R}{2}}+\dfrac{1}{R}=\dfrac{2}{R} \\\ & {{R}_{eq}}=\dfrac{R}{2} \\\ \end{aligned}$

The equivalent resistance for part two is

${{R}_{eq}}=\dfrac{R}{2}+\dfrac{R}{2}=R$
The equivalent resistance for part three is

$\begin{aligned} &\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{R+\dfrac{R}{2}}+\dfrac{1}{R}=\dfrac{2}{3R}+\dfrac{1}{R}=\dfrac{5}{3R} \\\ & {{R}_{eq}}=\dfrac{3R}{5} \\\ \end{aligned}$

But we know that current always flows through the least resistance path, so the current would be short circuited back from the third part of the circuit. This means no current reaches part one and two of the circuit.
Thus the equivalent resistance of the circuit is
${{R}_{eq}}=\dfrac{R}{3}+\dfrac{R}{2}+\dfrac{R}{2}=\dfrac{4R}{3}$
We have to apply Ohm’s Law i.e.,

$V=IR$
$\Rightarrow I=\dfrac{3V}{4R}$
Hence the answer is option B.

Note:
The possibility of making a mistake in this question is by reducing the entire circuit and considering all the resistors to find the equivalent resistance. The ohm's law used here states that the voltage across a resistor is directly proportional to the amount of current flowing through it. Current flowing through all the resistors connected in series is the same while the voltage is different. Voltage across each resistor connected in parallel is the same while current is different.