Question

Find the ratio in which the segment joining the points (1,-3) and (4,5) is divided by the x axis. Also, find the coordinates of this point on the x axis.

Answer 1

This question involves the concepts of section formula of straight line. In this question, we have to assume the ratio as m:n and then by using the formula we will calculate the ratio and also get the coordinates of the point P. We will use the section formula. If AB is a line segment and has coordinates $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ and a point P (a,b) divides AB in the ratio, m:n, then we can represent it as follows.

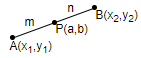
So, according to the section formula, we get,
$a=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},b=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$

Complete step by step answer:
Now, let us assume that the line segment AB joining the points (1,-3) and (4,5) is divided in the ratio m:n by the x axis.
So, let the point P which is on x-axis and dividing the line AB, have the co-ordinates $\left( {{a}_{1}},0 \right)$. So, we can represent it as follows.

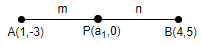
Now, we know that section formula is given as, $a=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},b=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$, where (a,b) is coordinate of the point dividing the line segment in the ratio m:n and $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ are the coordinates of the points joining the line segment.
We can consider the point A as $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,-3 \right)$ and the point B as $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 4,5 \right)$.
So, by section formula, we get the y coordinate of the point P as,
y – coordinate of P $=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$
Now, we know that the y coordinate of point P is equal to 0. And also we have ${{y}_{1}}=-3,{{y}_{2}}=5$. So, on substituting these values in the above formula, we get,
$0=\dfrac{m\left( 5 \right)+n\left( -3 \right)}{m+n}$
On cross multiplying we get,
$0=5m-3n$
So, we can write it,
$5m=3n$
On transposing n from the RHS to LHS and 5 from the LHS to the RHS, we get,
$\dfrac{m}{n}=\dfrac{3}{5}$
Thus, we get the ratio of m:n as,
m:n = 3:5
Now, we will find the x coordinate of the point P using the section formula, so we get,
x – coordinate of P $=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$
Know, we have the x coordinate of point P as ${{a}_{1}}$ and also we have, ${{x}_{1}}=1,{{x}_{2}}=4,m=3,n=5$. So, on substituting these values in the above formula, we get,
$\begin{aligned} & {{a}_{1}}=\dfrac{3\times 4+5\times 1}{3+5} \\\ & {{a}_{1}}=\dfrac{\begin{aligned} & 12+5 \\\ \end{aligned}}{8} \\\ & {{a}_{1}}=\dfrac{17}{8} \\\ \end{aligned}$
Hence, we get the coordinates of point P as $\left( \dfrac{17}{8},0 \right)$.

Therefore, the x axis divides the line AB in the ratio 3:5 at point $\left( \dfrac{17}{8},0 \right)$.

Note: While solving this question, the students must remember that the section formula is $a=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},b=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$, where (a,b) is coordinate of the point dividing the line segment in the ratio m:n and $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ are the coordinates of the points joining the line segment.
Often, the students make mistake while writing this formula, and may write it as $a=\dfrac{m{{x}_{1}}+n{{x}_{2}}}{m+n},b=\dfrac{m{{y}_{1}}+n{{y}_{2}}}{m+n}$, but this is wrong and will result in the wrong answer.
Also, sometimes, the ratio m:n, we get can be negative, like $\dfrac{m}{n}=-\dfrac{3}{5}$, but we shouldn’t neglect this, as this ratio is also correct and it represents the external division of line.