Question

Find the ratio in which the point (- 3, p) divides the line segment joining the points (-5, -4) and (-2, 3). Hence, find the value of p.

Answer 1

Hint: In this question to find the values of p, we will assume that the point (-3, p) divides the line joining the points (-5, -4) and (-2, 3) in the ratio of k : 1. And will use the section formula to find the value of p and k.

Complete step-by-step solution -

Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let say A (-5, -4) and B (-2, 3) makes a line segment AB. The line segment AB is divided at point Q, so, we will apply section formula at point Q.
Let Q (-3, p) divide the line segment AB in the ratio k : 1.
So, applying section formula at point Q (-3, p), we get
x – coordinate of Q = $\dfrac{{k\left( { - 2} \right) + 1\left( { - 5} \right)}}{{k + 1}}$ = $\dfrac{{ - 2k - 5}}{{k + 1}}$
y – coordinate of Q = $\dfrac{{k\left( 3 \right) + 1\left( { - 4} \right)}}{{k + 1}} = \dfrac{{3k - 4}}{{k + 1}}$
Now as we know that the coordinates of point Q is (-3, p)
So, on comparing the x – coordinate of point Q. We get,
$\dfrac{{ - 2k - 5}}{{k + 1}} = - 3$
Cross-multiplying above equation to find the value of k. We get,
– 2k – 5 = – 3(k + 1)
– 2k – 5 = – 3k – 3
Adding 3k + 5 to both the sides of the above equation. We get,
k = 2
Now to find the value of p we had to compare the y -coordinate of point Q with p and put the value of k = 2.
So, p = $\dfrac{{3k - 4}}{{k + 1}}$
Now putting the value of k as 2 in the RHS of the above equation. We get,
p = $\dfrac{{3\left( 2 \right) - 4}}{{2 + 1}} = \dfrac{2}{3}$
Hence, the point $\left( { - 3,\dfrac{2}{3}} \right)$ divides the line segment joining the points (-5, -4) and (-2, 3) in ratio 2 : 1.

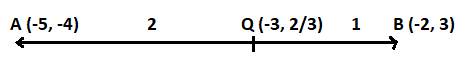
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.