Question

Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6)?

Answer 1

Let us assume the ratio be $\left( {{m}_{1}}:{{m}_{2}} \right)$ which is formed when (-1, 6) divides the line segment joining the points (-3, 10) and (6, -8). Now, we are going to use the section formula to find the values of $\left( {{m}_{1}}\And {{m}_{2}} \right)$. We know that if we have two points say, $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ and there is a point say $\left( a,b \right)$ which divides it into the ratio $\left( {{m}_{1}}:{{m}_{2}} \right)$ then the relation between them is as follows:
$\begin{aligned} & a=\dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}}; \\\ & b=\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$

Complete step by step answer:
Let us draw a line segment with two points (-3, 10) and (6, -8) and a point (-1, 6) which lies on the line segment.

Now, let us assume the ratio in which C divides A and B is $\left( {{m}_{1}}:{{m}_{2}} \right)$. Marking this ratio in the above diagram we get,

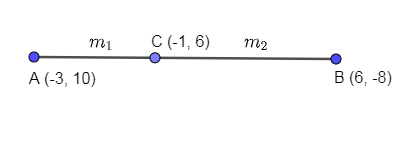
To find the values of $\left( {{m}_{1}}\And {{m}_{2}} \right)$, we are going to use the section formula. Now, let us see how the section formula is used. Let us consider two points $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ and there is a point say $\left( a,b \right)$ which divides it into the ratio $\left( {{m}_{1}}:{{m}_{2}} \right)$ then the relation between them is as follows:
$\begin{aligned} & a=\dfrac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}}; \\\ & b=\dfrac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$
Now, let us take $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ as (-3, 10) and (6, -8) respectively. And point $\left( a,b \right)$ as (-1, 6). Substituting these values in the above formula we get,
$\begin{aligned} & -1=\dfrac{{{m}_{1}}\left( 6 \right)+{{m}_{2}}\left( -3 \right)}{{{m}_{1}}+{{m}_{2}}}; \\\ & 6=\dfrac{{{m}_{1}}\left( -8 \right)+{{m}_{2}}\left( 10 \right)}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$
Cross-multiplying the above two equations we get,
$\begin{aligned} & -1\left( {{m}_{1}}+{{m}_{2}} \right)=6{{m}_{1}}-3{{m}_{2}} \\\ & \Rightarrow -{{m}_{1}}-{{m}_{2}}=6{{m}_{1}}-3{{m}_{2}} \\\ & \Rightarrow 2{{m}_{2}}=7{{m}_{1}}.....(1) \\\ \end{aligned}$
$\begin{aligned} & 6\left( {{m}_{1}}+{{m}_{2}} \right)=-8{{m}_{1}}+10{{m}_{2}} \\\ & \Rightarrow 6{{m}_{1}}+6{{m}_{2}}=-8{{m}_{1}}+10{{m}_{2}} \\\ & \Rightarrow 14{{m}_{1}}=4{{m}_{2}}....(2) \\\ \end{aligned}$
Dividing eq. (2) by 2 we get,
$7{{m}_{1}}=2{{m}_{2}}$
Rearranging the above equation we get,
$\dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{2}{7}$
Writing the fraction in the ratio form we get,
${{m}_{1}}:{{m}_{2}}=2:7$
Hence, we have found the ratio as 2:7.

Note: In the above solution, as you can see both the equations (1 and 2) are giving the same ratio value so you can solve one of the two equations and get the value of the ratio. There is no need to solve both the equations. Having this information in mind that both the equations will give the same ratio values can reduce the solving time in examination.