Question

Find the ratio in which the line segment joining the points A (3, -3) and B (-2, 7) is divided by the x-axis. Two times the x-coordinate of the point of division is

Answer 1

Hint: In this question, the concept is that any coordinate on the x axis is (x, 0). Then use the section formula to calculate the ratio and the x-coordinate of the point of division.

Complete step-by-step answer:

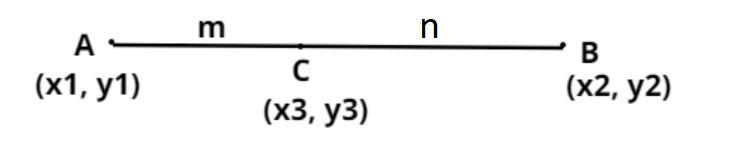
Let us suppose that the line segment joining the points A and B is divided by the x-axis in the ratio (m : n) as shown in figure.
So C is the point which lies on the x-axis.

Now as we know that on x-axis the coordinate of y is zero.
Therefore (y3 = 0)
So the coordinates of C = (x3, 0)
Now let A = (x1, y1) = (3, -3)
And B = (x2, y2) = (-2, 7)

So according to section formula the coordinates of C is written as
${x_3} = \dfrac{{m.{x_2} + n.{x_1}}}{{m + n}},{y_3} = \dfrac{{m.{y_2} + n.{y_1}}}{{m + n}}$
Now substitute all the values in this equation we have,
${x_3} = \dfrac{{m\left( { - 2} \right) + 3n}}{{m + n}}..........\left( 1 \right)$
And
$0 = \dfrac{{7m + n\left( { - 3} \right)}}{{m + n}}...........\left( 2 \right)$

Now simplify first equation (2) we have,
$0\left( {m + n} \right) = 7m + n\left( { - 3} \right)$
$\Rightarrow 7m - 3n = 0$
$\Rightarrow 7m = 3n$......................... (3)
$\Rightarrow \dfrac{m}{n} = \dfrac{3}{7}$
So this is the required ratio in which the line segment joining the points A and B divides by x-axis.

Now from equation (1) we have,
${x_3} = \dfrac{{ - 2m + 3n}}{{m + n}}$
From equation (3) we have,
${x_3} = \dfrac{{ - 2m + 7m}}{{m + \dfrac{{7m}}{3}}} = \dfrac{{15m}}{{10m}} = \dfrac{3}{2}$
So the coordinates of the x-axis is $\left( {\dfrac{3}{2},0} \right)$

Now we have to calculate the two times the x-coordinate of the point of division.
So simply multiply by 2 in the x-coordinate.
Therefore two times the x-coordinate of the point of division is (3, 0).
So this is the required answer.

Note: In this question firstly we have founded out the ratio in which the line segment is divided by the x-axis. Using this ratio we are able to find the x coordinate of the point on x-axis which is dividing the line segment. Twice the x coordinate can easily be found by simply multiplying the x coordinate with two.