Question

Find the ratio in which the line segment joining A (1, – 5) and B (– 4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.

Answer 1

Hint: In order to solve this question, we should have some knowledge of section formula, that is when two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are divided by any point (h, k) in the ratio m:n, then we can say, $h=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $k=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$.

Complete step-by-step answer:
In this question, we have to find the coordinates of a point that lies on the x-axis and divide the line joining points A (1, – 5) and B (– 4, 5) and also the ratio in which the point divides the line. Let the ratio in which the point divides the line be m:1. And we know that when a point lies on the x-axis then its y – coordinate is 0, which means the coordinates of a point of division are (h, 0) where h is the x coordinate.

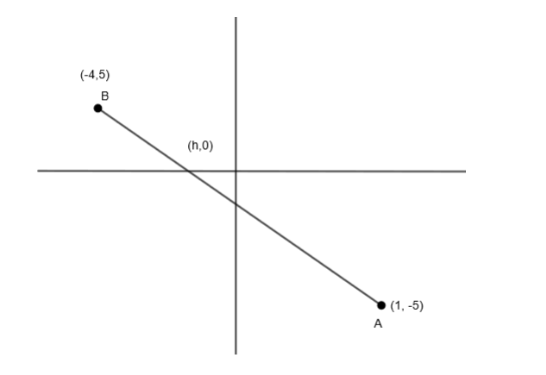
Now, we know that when two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are divided by any point (h, k) in ratio m:n, then we can say, $h=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $k=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$. So, for points A (1, – 5) and B (– 4, 5), point (h, 0) divides in the ratio m:1, we can write,
$h=\dfrac{m\left( -4 \right)+1\left( 1 \right)}{m+1}....\left( i \right)$
And, $0=\dfrac{m\left( 5 \right)+1\left( -5 \right)}{m+1}....\left( ii \right)$
Now, from equation (ii), we will find out the value of m. So, we will get,
$0=\dfrac{5m-5}{m+1}$
Now, we will cross multiply the equation. So, we will get,
$0=5m-5$
$5m=5$
$m=1.....\left( iii \right)$
So, we get the ratio as 1:1.
Now, from equation (iii), we will put the value of m in equation (i). So, we will get,
$h=\dfrac{1\left( -4 \right)+1\left( 1 \right)}{1+1}$
Now, we will simplify it to find the value of h. So, we will get,
$h=\dfrac{-4+1}{2}$
$h=\dfrac{-3}{2}$
Hence, we can say that the coordinates of the point which divides the line joining A (1, – 5) and B (– 4, 5) in the ratio 1:1 is $\left( \dfrac{-3}{2},0 \right)$

Note: In such types of questions, the general mistake which students make is assuming m:1 and at the time of using it in the formula, students tend to use it as 1:m,such mistakes should be avoided and there must be clarity of m,n values.