Question

Find the ratio in which the line $2x + 3y - 5 = 0$ divides the line segment joining the points $\left( {8, - 9} \right)$ and $\left( {2,1} \right)$ . Also find the coordinates of the point of division.

Answer 1

Hint : In the given problem, we are asked to find the ratio and co-ordinates of the point of division such that the line $2x + 3y - 5 = 0$ divides the line segment joining the points $\left( {8, - 9} \right)$ and $\left( {2,1} \right)$ . In order to find the ratio we will use a section formula.

Complete step by step solution:
In this given problem, the line of equation is $2x + 3y - 5 = 0$ . Let $A\left( {{x_1},{y_1}} \right) = \left( {8, - 9} \right)$ and $B\left( {{x_2},{y_2}} \right) = \left( {2,1} \right)$ be the end points of line segment $AB$ and $P\left( {x,y} \right)$ be the point of division of line segment joining the $AB$ .

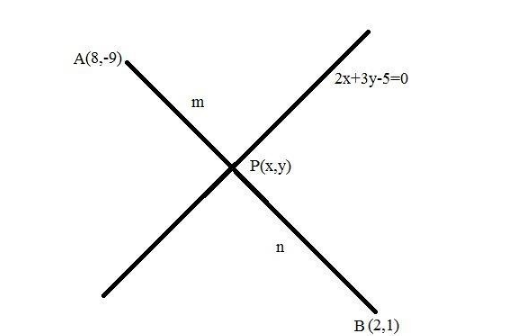
Let us assume that the ratio in which $P$ divides $AB$ is $m:n = k:1$ . Therefore, by using section formula coordinates of $P$ is
$P\left( {x,y} \right) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) \\\ \Rightarrow P\left( {x,y} \right) = \left( {\dfrac{{2k + 8}}{{k + 1}},\dfrac{{k - 9}}{{k + 1}}} \right) \;$
We know that $P$ lies on the line $2x + 3y - 5 = 0$ . Hence it will satisfy the equation of line. Therefore, we can write
$2\left( {\dfrac{{2k + 8}}{{k + 1}}} \right) + 3\left( {\dfrac{{k - 9}}{{k + 1}}} \right) - 5 = 0 \\\ \Rightarrow 2\left( {\dfrac{{2k + 8}}{{k + 1}}} \right) + 3\left( {\dfrac{{k - 9}}{{k + 1}}} \right) = 5 \\\$
Now we take $\dfrac{1}{{k + 1}}$ common in the left hand side of the equality sign and then multiplied both sides by $k + 1$ . Then, we get
$2\left( {2k + 8} \right) + 3\left( {k - 9} \right) = 5\left( {k + 1} \right)$
Let us simplify the above equation and find the value of $k$ . Therefore, we can write
$4k + 16 + 3k - 27 = 5k + 5 \\\ \Rightarrow 4k + 3k - 5k = 5 + 27 - 16 \\\ \Rightarrow 2k = 16 \\\ \Rightarrow k = \dfrac{{16}}{2} \\\ \Rightarrow k = 8 \;$
Let us put $k = 8$ in $P\left( {x,y} \right) = \left( {\dfrac{{2k + 8}}{{k + 1}},\dfrac{{k - 9}}{{k + 1}}} \right)$ . Therefore, we get $P\left( {x,y} \right) = \left( {\dfrac{{24}}{9}, - \dfrac{1}{9}} \right)$
Therefore, we can say that the ratio in which the line $2x + 3y - 5 = 0$ divided the line segment joining the point $\left( {8, - 9} \right)$ and $\left( {2,1} \right)$ is $k:1 = 8:1$ and coordinates of point $P$ is given by $\left( {x,y} \right) = \left( {\dfrac{{2k + 8}}{{k + 1}},\dfrac{{k - 9}}{{k + 1}}} \right) = \left( {\dfrac{{24}}{9},\dfrac{{ - 1}}{9}} \right)$ .
So, the correct answer is “ $\left( {\dfrac{{24}}{9},\dfrac{{ - 1}}{9}} \right)$ .”

Note : According to the section formula, the coordinates of the point $P\left( {x,y} \right)$ which divides the line segment joining the point $A\left( {{x_1},{y_1}} \right)$ and $B\left( {{x_2},{y_2}} \right)$ in the ratio ${m_1}:{m_2}$ internally, is $\left( {\dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_1} + {m_2}{y_2}}}{{{m_1} + {m_2}}}} \right)$ . Then by using this ratio we will find the coordinates of the point of division. If the midpoint of a line segment divides the line segment in the ratio $1:1$ then the coordinates of the mid-point $P$ is $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$ .