Question
Question: Find the ratio in which the join of the points \(\left( { - 1,3} \right)\) and \(\left( {1,5} \right...
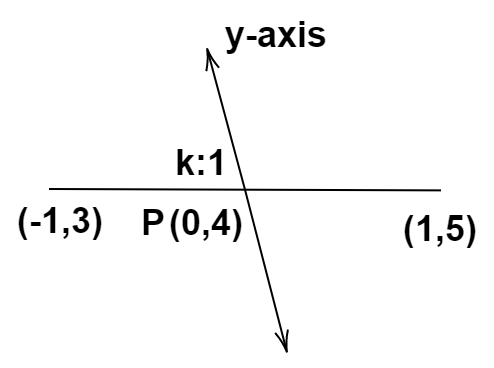
Find the ratio in which the join of the points (−1,3) and (1,5) is divided by the y axis.
Solution
In the given question, we are required to find the ratio in which a line divides the join of two points whose coordinates are given to us. Firstly, we find the coordinates of a point at which the line divides the line segment joining the two given points. Then, we find out the ratio in which the join of the two points is divided. The required task can be done using the section formula where we can use a predefined formula given the coordinates of the end points of the line segment and the coordinates of the point at which the line divides the join of endpoints.
Complete step by step answer:
We are given the points (−1,3) and (1,5).
We find out the equation of the line passing through these two points.
We know the two point form of the line, where we can find the equation of a straight line given the coordinates of two points lying on it. The two point form of the line can be represented as: (y−y1)=(x2−x1)(y2−y1)(x−x1) where (x1,y1) and (x2,y2) are the coordinates of the two points.
So, the equation of the line passing through (−1,3) and (1,5) is (y−3)=(1−(−1))(5−3)(x−(−1)).
Now, simplifying the equation of the straight line, we get,
⇒(y−3)=22(x+1)
Opening the brackets, we get,
⇒y−3=x+1
⇒y=x+4
Now, the equation of the other line is the y axis. So, the equation is x=0.
Now, we find the point of intersection of these two lines by solving the equations of both.
Substituting the value of x from equation x=0 into the equation y=x+4, we get,
⇒y=0+4
⇒y=4
So, the coordinates of the point at which y axis divides the join of (−1,3) and (1,5) are (0,4).
Now, we have to find the ratio in which the join of the endpoints (−1,3) and (1,5) is divided at the point (0,4).
So, let the ratio in which the point (0,4) divides the line segment be k:1.
Using section formula, Coordinates of point P =(m+nnx1+mx2,m+nny1+my2), where (x1,y1) and (x2,y2) are the coordinates of the endpoints of the line segment and m:n is the ratio in which the Point P divides the line segment.
So, Coordinates of Point P =(k+11(−1)+k(1),k+11(3)+k(5))
Opening the brackets and simplifying the calculations, we get,
=(k+1−1+k,k+13+5k)
Now, equating this with the actual coordinates of Point P found already as (0,4), we get,
k+1k−1=0 and k+13+5k=4
⇒k−1=0 and ⇒3+5k=4(k+1)
⇒k=1 and ⇒3+5k=4k+4
⇒k=1 and ⇒k=1
Hence, the value of k comes out to be 1 from both the equations.
Hence, the ratio in which the join of the points (−1,3) and (1,5) is divided by the y axis is 1:1.
Note:
We must remember the section formula and its applications in order to solve the problem. The division of join of two points in the ratio 1:1 means that the point at which the division of the line occurs is also the midpoint of the line. We can also notice that using the midpoint formula as (2x1+x2,2y1+y2).
Substituting the coordinates x1=−1, y1=3, x2=1 and y2=5, we get,
(2−1+1,23+5)
⇒(0,4)
So, the point (0,4) is the midpoint of the join of points (−1,3) and (1,5).
