Question

Find the range of projectile on the inclined plane which is projected perpendicular to the inclined plane with velocity $20m/s$ as shown in the figure:

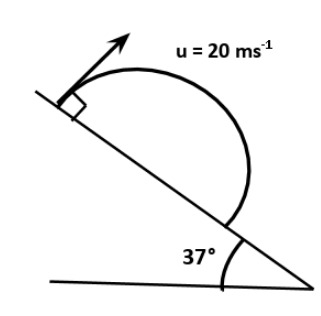
A. $55m$
B. $75m$
C. $84m$
D. $100m$

Answer 1

The projectile is projected perpendicular to the inclined plane with a certain velocity. Due to its acceleration and gravity, the projectile will form a parabolic path. It is shown in the figure, that the projectile hits the end of the inclined plane at the end of the parabolic path. Calculating the distance covered by the projectile on the inclined plane will give the range of the projectile.

Formula Used:
The time of flight of projectile $T$ is given by:
$T = \dfrac{{2u\sin (\alpha - \beta )}}{{g\cos \beta }}$
The distance covered by the projectile $D$ along an inclined plane is given by:
$D = \dfrac{{2{u^2}\sin (\alpha - \beta )\sin \alpha }}{{g{{\cos }^2}\beta }}$
where, $\beta$ is the angle of the inclined plane with the horizontal, $\alpha$ is the angle of projection of the projectile, $g$ is the acceleration due to gravity and $u$ is the initial velocity of the projectile.

Complete step by step answer:
The given figure shows an inclined plane making an angle $\beta$ with the horizontal. Therefore, $\beta = {37^ \circ }$. A body is thrown with velocity $u$ making an angle $\alpha$ with the horizontal from the inclined plane. It is given that the projectile is projected perpendicular to the inclined plane. Therefore, $\alpha = {90^ \circ }$. The projectile thus thrown will strike somewhere at the bottom of the inclined plane. This distance covered by the projectile is called the range of the projectile.

The motion of a projectile is a parabola. The velocity of the projectile along the inclined plane is $u\cos (\alpha - \beta )$and that perpendicular to the plane is $u\sin (\alpha - \beta )$. The time of flight of projectile $T$ is given by
$T = \dfrac{{2u\sin (\alpha - \beta )}}{{g\cos \beta }}$
where, $\beta = {37^ \circ }$, $\alpha = {90^ \circ }$ and $g$ is the acceleration due to gravity.
Therefore, $T = \dfrac{{2\left( {20} \right)\sin ({{90}^ \circ } - {{37}^ \circ })}}{{10\left( {\cos {{37}^ \circ }} \right)}}$

Solving in parts
$\sin (\alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta$
Here, $\beta = {37^ \circ }$ and $\alpha = {90^ \circ }$. Therefore

$$\sin ({90^ \circ } - {37^ \circ }) = \sin {90^ \circ }\cos {37^ \circ } - \cos {90^ \circ }\sin {37^ \circ } \\\ \Rightarrow \sin ({90^ \circ } - {37^ \circ }) = \left( {1 \times 0.7986} \right) + \left( {0 \times 0.6018} \right) \\\ \Rightarrow \sin ({90^ \circ } - {37^ \circ }) = 0.7986 \\\$$

Thus, $T = \dfrac{{2\left( {20} \right) \times 0.7986}}{{10\left( {0.7986} \right)}} = 4s$. Hence, the time of flight of the projectile will be 4 seconds.
The distance covered by the projectile $D$ along an inclined plane is given by;

D = \dfrac{{2{u^2}\sin (\alpha - \beta )\sin \alpha }}{{g{{\cos }^2}\beta }} \\\ \Rightarrow D = \dfrac{{2{{\left( {20} \right)}^2}\sin ({{90}^ \circ } - {{37}^ \circ })\sin {{90}^ \circ }}}{{10 \times {{\cos }^2}\left( {{{37}^ \circ }} \right)}} \\\ \Rightarrow D = \dfrac{{800 \times 0.7986 \times 1}}{{10 \times 0.6378}} \\\ \therefore D = 100m $$ **Hence, option D is the correct answer.** **Note:** The mass of the object performing the projectile motion is not considered here. When the projectile is projected perpendicular to the inclined plane with a certain velocity, then it is totally under the gravitational force of influence. Due to this, all bodies fall freely with the same acceleration. The acceleration of the falling bodies does not depend on the mass of the body.If the object is projected with a certain velocity, it is assumed that the friction of air is negligible.