Question

Find the range of c which the line $y = mx + c$ touches the parabola ${y^2} = 8\left( {x + 2} \right)$.

Answer 1

Hint : Use both the given equation to eliminate ‘y’ and form an quadratic equation in term of ‘x’ and then equating discriminant of quadratic equation equal to zero as line is given tangent to parabola and then solving ‘c’ for discriminant greater than zero to find its range.

Complete step-by-step answer :

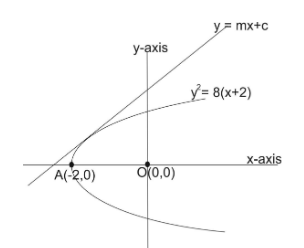
From the statement we have line $y = mx + c$ touches the parabola ${y^2} = 8(x + 2)$ .
Using, value of y from line in equation of parabola we have,
${(mx + c)^2} = 8x + 16$
$\Rightarrow {m^2}{x^2} + {c^2} + 2mxc = 8x + 16$
Shifting terms to the left hand side. We have,
$\Rightarrow {m^2}{x^2} + {c^2} + 2mcx - 8x - 16 = 0$
Forming quadratic in terms of ‘x’.
$\Rightarrow {m^2}{x^2} + (2mc - 8)x + ({c^2} - 16) = 0$
Since, the given line touches the parabola. Hence, there will be only one root possible.
$\therefore D = 0$ , where D is discriminant of the above formed quadratic equation.
${b^2} - 4ac = 0\,\,\,\,\,\,\,$
From quadratic equation we have $a = {m^2}{x^2},\,\,b = 2mc - 8,c = {c^2} - 16$
Substituting values of ‘a’, ‘b’ and ‘c’ in above formula. We have,
${(2mc - 8)^2} - 4 \times {m^2} \times ({c^2} - 16) = 0$
$\Rightarrow {(2mc)^2} + {(8)^2} - 2 \times (2mc) \times 8 - 4{m^2}({c^2} - 16) = 0$
$\Rightarrow 4{m^2}{c^2} + 64 - 32mc - 4{m^2}{c^2} + 64{m^2} = 0$
$\Rightarrow 64{m^2} - 32mc + 64 = 0$
$\Rightarrow 32(2{m^2} - mc + 2) = 0$
$\Rightarrow 2{m^2} - cm + 2 = 0$ , as $m \in R(range)$
So, $D \geqslant 0$ , here $a = 2,b = - c,c = 2$
{b^2} - 4ac \geqslant 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\\{ {\because D = {b^2} - 4ac} \right\\}
$\Rightarrow {(c)^2} - 4 \times 2 \times 2 \geqslant 0$
$\Rightarrow {c^2} - 16 \geqslant 0$
$\Rightarrow {c^2} \geqslant 0 + 16$
$\Rightarrow {c^2} \geqslant 16$
$\Rightarrow |c| \geqslant 4$
\Rightarrow c \geqslant 4\,\,\,and\,\,\,c \leqslant - 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\\{ {|x|\,\, \geqslant a \Rightarrow x > a\,\,and\,\,x \leqslant - a} \right\\}
$\Rightarrow c \in ( - \infty , - 4] \cup [4,\infty )$
Hence, from above we see that required range of ‘c’ is $( - \infty , - 4] \cup [4,\infty )$

Note : We know that not even for parabola but for all curves like circle, ellipse, hyperbola etc. Whenever a given line touches the given curve (parabola, ellipse, hyperbola…) then always solve for discriminant equal to zero of quadratic equation formed by eliminating ‘y’ from parabola using given equation of a line and then solve the equation so formed from equating discriminant equal to zero to get required solution of the given problem.