Question

Find the range for $\sinh x+\cosh x$ .
A. $\left( 1,\infty \right)$
B. $\left( 0,\infty \right)$
C. $\left( -\infty ,\infty \right)$
D. $\left( -\infty ,0 \right)$

Answer 1

Hint: Hyperbolic functions are analogs of the ordinary trigonometric functions defined for the hyperbola rather than on the circle. We know the formulae of $\sinh x=\dfrac{{{e}^{x}}-{{e}^{-x}}}{2}$ and $\cosh x=\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}$. By using these formulas first we have to evaluate the value of $\sinh x+\cosh x$.

Complete step-by-step answer:
We know hyperbolic functions are analogs of the ordinary trigonometric functions defined for the hyperbola rather than on the circle. The two basic hyperbolic functions are $\sinh x$ and $\cosh x$. And we also know the value of $\sinh x$ and $\cosh x$.
According to the formulae
$\sinh x=\dfrac{{{e}^{x}}-{{e}^{-x}}}{2}$
Now divide each value with “2” we get,
$\Rightarrow \left( \dfrac{{{e}^{x}}}{2}-\dfrac{{{e}^{-x}}}{2} \right)$

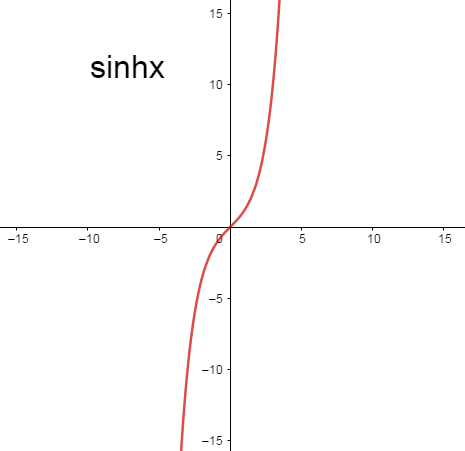
And,
$\cosh x=\dfrac{{{e}^{x}}+{{e}^{-x}}}{2}$
Now divide each value with “2” we get
$\Rightarrow \left( \dfrac{{{e}^{x}}}{2}+\dfrac{{{e}^{-x}}}{2} \right)$

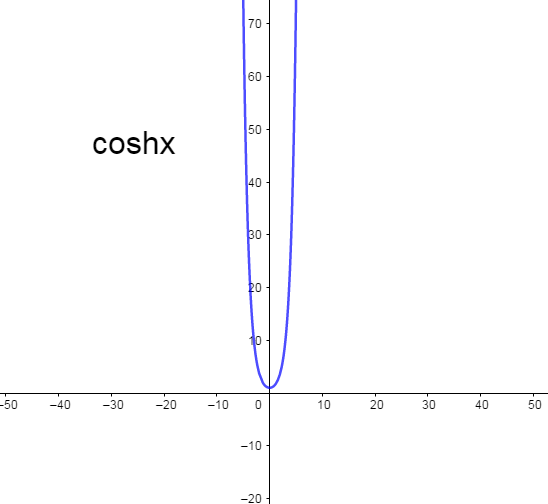
Now we have to calculate the range of $\sinh x+\cosh x$.
By adding the value of $\sinh x$ and $\cosh x$ we have,

& \sinh x+\cosh x \\\ & \Rightarrow \left( \dfrac{{{e}^{x}}}{2}-\dfrac{{{e}^{-x}}}{2} \right)+\left( \dfrac{{{e}^{x}}}{2}+\dfrac{{{e}^{-x}}}{2} \right) \\\ & \Rightarrow \dfrac{2{{e}^{x}}}{2} \\\ & \Rightarrow {{e}^{x}} \\\ \end{aligned}$$  Now we have to evaluate the range of $${{e}^{x}}$$. The domain is the subset of $$\mathbb{R}$$for which all operations in the function's formula make sense. Since $$e$$ is a positive real constant, it can be raised to any real power, so the domain is not limited. It is $$\mathbb{R}$$. Where $$\mathbb{R}$$ is the real number. Since a positive real constant is raised to a real power, the result is always positive, and is never equal to zero. If the power is to equal zero its base must equal zero, and its exponent must be different from zero it is not possible in that case. So the range is all positive real numbers without zero. So the range of the function is $$\left( 0,+\infty \right)$$(Option B). Note: Students have to understand the value of function and what is the value of $$\mathbb{R}$$. Students have to remember the hyperbolic functions formulae and they have to know how to draw the $$\sinh x$$ and $$\cosh x$$ graphs. Understanding of $$e$$ and how it works is also very important for solving this problem.