Question

Find the radius of gyration of a rod of mass m and length 2l about an axis passing through its ends and perpendicular to its length.

Answer 1

Radius of gyration is defined as the distance between the axis of rotation and the point where the total mass of the body is supposed to be concentrated. So, to find the radius of gyration, we can use the direct formula for radius of gyration which is dependent on the moment of inertia and mass of the rod. Initially, calculate the moment of inertia using its formula and then substitute it in the formula for radius of gyration. This obtained value will be the radius of gyration of the rod of mass m and length 2l.

Formula used:
$I = m{K}^{2}$
$I= \dfrac {1}{3}m{l}^{2}$

Complete answer:

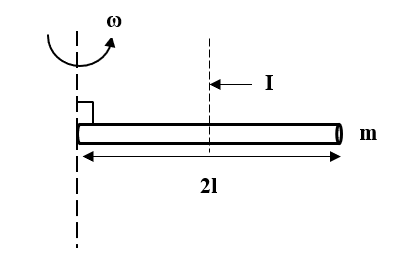
Given: Mass of rod = m
Length of the rod (l)= 2l
The formula for radius of gyration of a mass is given by,
$I = m{K}^{2}$ …(1)
Where, I is the Moment of inertia about the axis
K is the radius of gyration
Rearranging equation. (1) we get,
${K}^{2}= \dfrac {I}{m}$
$\Rightarrow K = \sqrt {\dfrac {I}{m}}$ …(2)
Moment of inertia of a rod passing through the end of the rod is given by,
$I= \dfrac {1}{3}m{l}^{2}$
Substituting the values in above equation we get,
$I= \dfrac {1}{3}m \times {2l}^{2}$
$\Rightarrow I= \dfrac {1}{3}m \times 4{l}^{2}$
Now, substituting the equation. (3) in equation. (2) we get,
$K= \sqrt {\dfrac { m \times 4{l}^{2}}{3m}}$
$\Rightarrow K= \dfrac {2l}{\sqrt{3}}$
Hence, the radius of gyration of the rod is $\dfrac {2l}{\sqrt{3}}$.

Note:
Radius of gyration depends on size and shape of the body. The body mass distribution of the object with respect to the rotational axis also influences the value of radius of gyration. If the body is close to the axis of rotation, then the value for radius of gyration will be less. If the body is away from the axis of rotation, then the value for the radius of gyration will be high. It’s S.I unit is meter.