Question

Find the probability of ${x^2} - 3x + 2 \geqslant 0$ in $x \in \left[ {0,5} \right]$.
A. $\dfrac{4}{5}$
B. $\dfrac{1}{5}$
C. $\dfrac{2}{5}$
D. $\dfrac{3}{5}$

Answer 1

Hint: To find the probability of the given equation, first we have to solve the inequality. After solving the inequality, draw it on a number line in the given boundaries. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
Given $x \in \left[ {0,5} \right]$
Consider ${x^2} - 3x + 2 \geqslant 0$
$\Rightarrow {x^2} - 3x + 2 \geqslant 0$
By splitting the terms of $x$, we have

$$\Rightarrow {x^2} - x - 2x + 2 \geqslant 0 \\\ \Rightarrow x\left( {x - 1} \right) - 2\left( {x - 1} \right) \geqslant 0 \\\ \Rightarrow \left( {x - 1} \right)\left( {x - 2} \right) \geqslant 0 \\\$$

We know that the inequality $\left( {x - a} \right)\left( {x - b} \right) \geqslant 0$ can be rewrite as $x \leqslant a{\text{ and }}x \geqslant b$
So, the inequality can be rewrite as
$x \leqslant 1{\text{ and }}x \geqslant 2$
If we draw it on number line, from points 0 to 5, we have

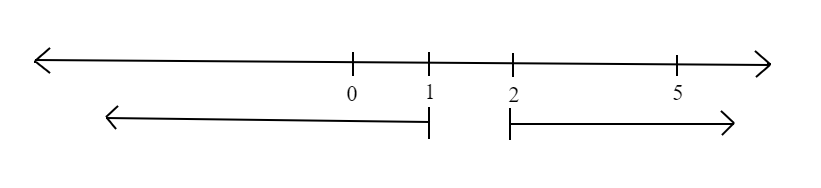
Clearly, from the number line diagram we can see that $\dfrac{4}{5}$ of the part is covered.
So, the required probability is $\dfrac{4}{5}$.
Thus, the correct option is A. $\dfrac{4}{5}$

Note: The probability of an event is always lying between 0 and 1 i.e., $0 \leqslant P\left( E \right) \leqslant 1$. Here the obtained answer is also lying between 0 and 1. Here students may forget to include boundary conditions.