Question

Find the principal value of the following: ${\sec ^{ - 1}}\left( {\dfrac{{ - 2}}{{\sqrt 3 }}} \right)$

Answer 1

Hint : Write the value of the trigonometric functions. The trigonometric function is the function that relates the ratio of the length of two sides with the angles of the right-angled triangle widely used in navigation, oceanography, the theory of periodic functions, and projectiles.

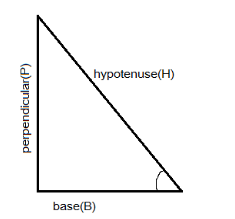
Commonly used trigonometric functions are the sine, the cosine, and the tangent, whereas the cosecant, the secant, the cotangent are their reciprocal, respectively. The value of these functions can be determined by the relation of the sides of a right-angled triangle where sine function is the ratio of perpendicular (P) and hypotenuses (H) of the triangle$\sin \theta {\text{ = }}\dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuses}}}}$. Cosine is the ratio of the base (B) and hypotenuses (H) of the triangle$\cos \theta {\text{ = }}\dfrac{{{\text{base}}}}{{{\text{hypotenuses}}}}$; the tangent is the ratio of the perpendicular (P) and base (B) of the triangle $\tan \theta {\text{ = }}\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$ , whereas ${\text{cosec }}\theta$ , $\sec {\text{ }}\theta$and $\cot {\text{ }}\theta$are their inverse respectively. The given value determines the value of these functions.

Complete step-by-step answer :

Function	$\sin \theta$	$\cos \theta$	$\tan \theta$
0	0	1	0
${30^0}$	$\dfrac{1}{2}$	$\dfrac{{\sqrt 3 }}{2}$	$\dfrac{1}{{\sqrt 3 }}$
${45^0}$	$\dfrac{1}{{\sqrt 2 }}$	$\dfrac{1}{{\sqrt 2 }}$	1
${60^0}$	$\dfrac{{\sqrt 3 }}{2}$	$\dfrac{1}{2}$	$\sqrt 3$
${90^0}$	1	0	Indeterminate

Let ${\sec ^{ - 1}}\left( {\dfrac{{ - 2}}{{\sqrt 3 }}} \right)$be equal to $\theta$, hence we can write
$\sec \theta = \left( {\dfrac{{ - 2}}{{\sqrt 3 }}} \right)$
Since$\sec \theta = \dfrac{1}{{\cos \theta }}$, hence we can say
$\cos \theta = \dfrac{1}{{\left( { - \dfrac{2}{{\sqrt 3 }}} \right)}} = - \dfrac{{\sqrt 3 }}{2}$
Where
$\cos \theta = - \dfrac{{\sqrt 3 }}{2} = \dfrac{b}{h}$
Represent $\cos \theta$on the triangle

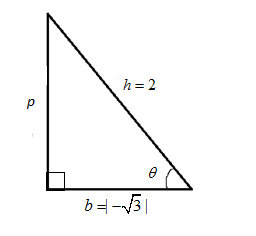
Now use Pythagoras theorem finds the perpendicular as

$$p = \sqrt {{h^2} - {b^2}} \\\ = \sqrt {{2^2} - {{\left( { - \sqrt 3 } \right)}^2}} \\\ = \sqrt {4 - 3} \\\ p = 1 \\\$$

Since, $\sin \theta = \dfrac{p}{h}$
Hence we get

$$\sin \theta = \dfrac{1}{2} \\\ \theta = {\sin ^{ - 1}}\left( {\dfrac{1}{2}} \right) \\\ = {30^ \circ } \\\$$

Note : Write the value of the function in the relation for the given respective angles in cases of${\text{cosec}}\theta$ $\sec \theta$, $\cot \theta$either inverse them or write their values, respectively. Alternatively, the given trigonometric function can be reduced to a smaller expression by carrying out general algebraic and trigonometric identities and at last put the values of the trigonometric functions for the respective values of $\theta$ .