Question

Find the principal value of ${\sec ^{ - 1}}( - 2)$.

Answer 1

In the given question, we have to apply trigonometric identities and rules of principal value to solve the question. If the equation involves a variable $0 \leqslant x \leqslant 2\pi$, then the solutions are called principal solutions.

Complete step by step solution:
In order to find the value of ${\sec ^{ - 1}}x$, we can follow the following steps:
Let $\sec \theta = x(\left| x \right| \geqslant 1,x \geqslant 1,x \leqslant - 1)$ then we will get:
$\theta = \sec - 1x$
Here $\theta$ has infinitely many values.
Let $0 \leqslant \alpha \leqslant \pi$ where:
$\alpha$ is $(\alpha \ne \dfrac{\pi }{2})$ non-negative smallest numerical value of these infinite number of values and satisfies the equation $\sec \theta = x$ then the angle $\alpha$ is called the principal value of ${\sec ^{ - 1}}x$.
Now let us solve the sum as follows:
Let $x = {\sec ^{ - 1}}( - 2)$
Using the property ${\sec ^{ - 1}}A = B$ so $\sec B = A$, we will get:
$\Rightarrow \sec x = - 2$
Using the trigonometric ratio table, we will get $\sec \dfrac{\pi }{3} = 2$. Thus, we will get:
$\Rightarrow \sec x = - \sec \dfrac{\pi }{3}$
Again, using the trigonometric ratio table, we will get $\operatorname{Sec} ( - 1) = \pi$ so we can conclude that:
$\Rightarrow \sec x = \sec (\pi - \dfrac{\pi }{3})$
Equalizing the denominator on the RHS, we get,
$\Rightarrow \sec x = \sec (\dfrac{{2\pi }}{3})$
Hence, we can get the value$x$ of as follows:
$\Rightarrow x = \dfrac{{2\pi }}{3}$
Since we have assumed $x = {\sec ^{ - 1}}( - 2)$, substituting the value, we will get,
$\Rightarrow {\sec ^{ - 1}}( - 2) = \dfrac{{2\pi }}{3}$
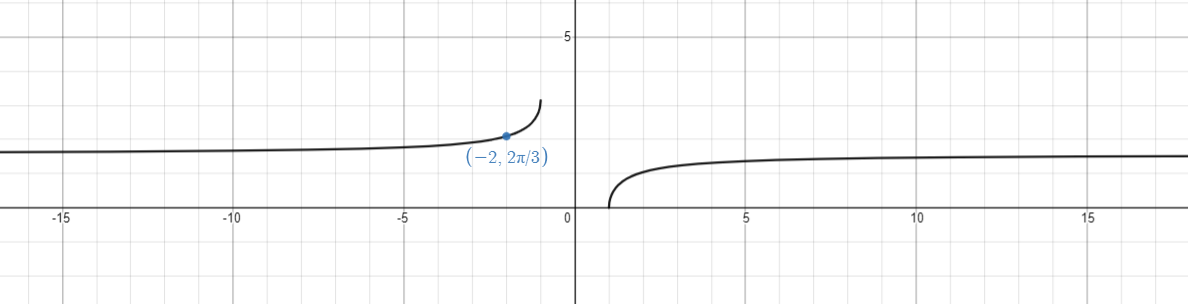
Thus, the principal value of ${\sec ^{ - 1}}( - 2)$ will be $\dfrac{{2\pi }}{3}$.
The following graph shows the principal value of ${\sec ^{ - 1}}( - 2)$.

Note:

1. If the principal value of ${\sec ^{ - 1}}x$ is $\alpha$, $(0 < \alpha < \pi )$ and $(\alpha \ne \dfrac{\pi }{2})$ then its general value = $2n\pi \pm \alpha$, where, $\left| x \right| \geqslant 1$.
   Therefore, ${\sec ^{ - 1}}x = 2n\pi \pm \alpha$, where, $(0 \leqslant \alpha \leqslant \pi )$, $\left| x \right| \geqslant 1$ and $\alpha \ne \dfrac{\pi }{2}$.
   In the given sum, the general value of ${\sec ^{ - 1}}( - 2)$ will be $2n\pi \pm \dfrac{{2\pi }}{3}$after solving the principal value.
2. ${\sec ^{ - 1}}A = B$ is simplified by simple cross multiplication as follows:
   ${\sec ^{ - 1}}A = B$ can be rewritten as-
   $\dfrac{1}{{\sec }}A = B$
   Cross-multiplying on the other side, we will get,
   $A = \sec B$
3. When there are two values, one is positive and the other is negative such that they are numerically equal, then the principal value is the positive one. For example, ${\sin ^{ - 1}}(x)$with domain $( - 1,1)$ will have range of $( - \dfrac{\pi }{2},\dfrac{\pi }{2})$.