Question

Find the principal value of $se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)$

Answer 1

Hint: First of all, consider the principal value of $se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)$ as y. Now, write $\dfrac{3\pi }{4}=\pi -\dfrac{\pi }{4}$ and use $\sin \left( \pi -\theta \right)=\sin \theta$ and table of trigonometric ratios to find the value of $2\sin \dfrac{3\pi }{4}$. Now, take sec on both the sides and use the trigonometric ratios table to find the principal value of the given expression.

Complete step-by-step answer:
Here, we have to find the principal value of $se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)$. Let us take the principal value of $se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)$ as y. So, we get,
$y=se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)$
Now by taking sec on both sides of the above equation, we get,
$secy=sec\left[ se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right) \right]$
We know that $sec\left( se{{c}^{-1}}x \right)=x$. By using this in the RHS of the above equation, we get,
$secy=2\sin \left( \dfrac{3\pi }{4} \right)$
We can also write the above equation as
$secy=2\sin \left( \pi -\dfrac{\pi }{4} \right)$
We know that $\sin \left( \pi -\theta \right)=\sin \theta$. By using this in the above equation, we get,
$secy=2\sin \left( \dfrac{\pi }{4} \right).....\left( i \right)$
Now, let us find the value at which $\sin \left( \dfrac{\pi }{4} \right)$ from the table below.

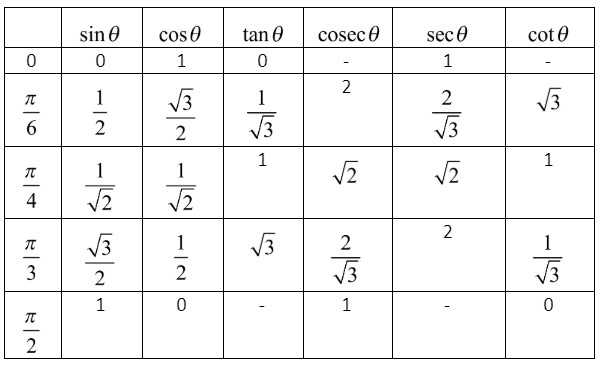
From the above table, we can see that $\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$. So by substituting the value of $\sin \dfrac{\pi }{4}$ in equation (i), we get
$\sec y=2.\dfrac{1}{\sqrt{2}}$
$\sec y=\sqrt{2}$
From the table we know that
$\cos\dfrac{\pi}{4}=\dfrac{1}{\sqrt{2}}$ and we know that $\cos\theta=\dfrac{1}{\sec\theta}$
We can write $\sec \dfrac{\pi }{4}=\sqrt{2}$. So by substituting the value of $\sqrt{2}$ in terms of sec in the above equation, we get,
$\sec y=\sec \dfrac{\pi }{4}$
By taking ${{\sec }^{-1}}$ on both the sides of the above equation, we get,
${{\sec }^{-1}}\left( \sec y \right)={{\sec }^{-1}}\left( \sec \dfrac{\pi }{4} \right)$
Now we know that the range of principal values of $se{{c}^{-1}}$ is $\left[ 0,\pi \right]-\dfrac{\pi }{2}$ and for this value ${{\sec }^{-1}}\left( \sec 0 \right)=0$. By applying this in the above equation, we get,
$y=\dfrac{\pi }{4}$
Hence, we get the principal value of $se{{c}^{-1}}\left( 2\sin \left( \dfrac{3\pi }{4} \right) \right)$ as $\dfrac{\pi }{4}$.

Note: First of all, in these type of questions, students must remember the value of at least $\sin \theta ,\cos \theta$ and $\tan \theta$ at general angles like ${{0}^{o}},{{30}^{o}},{{45}^{o}}$, etc. as values of $\sec \theta ,\operatorname{cosec}\theta ,\cot \theta$ could be found from these. Students should also verify their answer by substituting the value of y in the initial equation and checking if LHS = RHS. Also, take care whether the answer lies in the range of ${{\sec }^{-1}}$ or not and if it is a principal solution that is between 0 to $2\pi$ or not.