Question

Find the principal argument of the complex number $1 + \sqrt 2 + i$. Choose the correct option.
A. $\dfrac{\pi }{3}$
B. $\dfrac{\pi }{6}$
C. $\dfrac{\pi }{8}$
D. $\dfrac{\pi }{4}$

Answer 1

The complex number $z$ is of the form $z = x + iy$ where $x$ represents the real part and $y$ represents the imaginary part. In the given question, $z = 1 + \sqrt 2 + i$ has both real and imaginary parts that is $x = 1 + \sqrt 2$ is the real part of the complex number and $y = 1$ is the imaginary part of the given complex number. Use the formula of finding the principal argument of the complex number to find the argument of $z$. Use the Pythagoras theorem to find the value of $\theta$.

Complete step by step solution:
Consider the given complex number $z = x + iy$ which has both the parts in it. The real part is $x = 1 + \sqrt 2$ and the imaginary part is $y = 1$.
We know that, for a complex number $z = x + iy$, the principal argument of the complex number is given by $\arg \left( z \right) = {\tan ^{ - 1}}\left( {\dfrac{y}{x}} \right)$.
Next, we will substitute the values in the formula of principal argument of $z$.
Thus, we get,
$\arg \left( {1 + \sqrt 2 + i} \right) = {\tan ^{ - 1}}\left( {\dfrac{1}{{1 + \sqrt 2 }}} \right)$
Now, we will find the value of ${\tan ^{ - 1}}\left( {\dfrac{1}{{1 + \sqrt 2 }}} \right)$ by multiplying the numerator and denominator by $1 - \sqrt 2$
Thus, we get,
$\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{1}{{1 + \sqrt 2 }} \times \dfrac{{1 - \sqrt 2 }}{{1 - \sqrt 2 }}} \right)$
Next, we will use the property $\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}$ in the denominator.
Hence, we get,
$\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{{1 - \sqrt 2 }}{{1 - 2}}} \right) = {\tan ^{ - 1}}\left( {\sqrt 2 - 1} \right)$
Now, we will find the value of ${\tan ^{ - 1}}\left( {\sqrt 2 - 1} \right) = \theta$
$\Rightarrow \tan \left( \theta \right) = \sqrt 2 - 1$
Consider the figure,

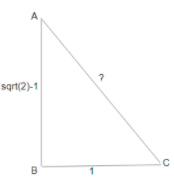
From this we have, $AB = \sqrt 2 - 1$ and $BC = 1$ and we have to find the value of $AC = ?$.
Using the Pythagoras theorem, we know that for a $\Delta ABC$, ${\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}$
Thus, we get,

$$\Rightarrow {\left( {AC} \right)^2} = {\left( {\sqrt 2 - 1} \right)^2} + {\left( 1 \right)^2} \\\ \Rightarrow {\left( {AC} \right)^2} = 2 + 1 - 2\sqrt 2 + 1 \\\ \Rightarrow {\left( {AC} \right)^2} = 4 - 2\sqrt 2 \\\ \Rightarrow \left( {AC} \right) = \sqrt {4 - 2\sqrt 2 } \\\ \Rightarrow AC = \sqrt {4\left( {1 - \dfrac{{2\sqrt 2 }}{4}} \right)} \\\ \Rightarrow AC = 2\sqrt {1 - \dfrac{{\sqrt 2 }}{2}} \\\ \Rightarrow AC = 2\sqrt {1 - \dfrac{1}{{\sqrt 2 }}} \\\ \Rightarrow AC = 2\sqrt {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} \\\$$

Now, we have $AB = \sqrt 2 - 1$, $BC = 1$ and $AC = 2\sqrt {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}}$
Next, we will find the value of $\sin \theta = \dfrac{{AB}}{{AC}}$ and $\cos \theta = \dfrac{{BC}}{{AC}}$
Thus, we have,
$\Rightarrow \sin \theta = \dfrac{{\sqrt 2 - 1}}{{2\sqrt {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} }}$ and $\cos \theta = \dfrac{1}{{2\sqrt {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} }}$
Next, we will evaluate the value of $\sin \theta \cos \theta$

$$\sin \theta \cos \theta = \dfrac{{\sqrt 2 - 1}}{{2\sqrt {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} }} \times \dfrac{1}{{2\sqrt {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} }} \\\ = \dfrac{{\sqrt 2 - 1}}{{4\left( {\dfrac{{\sqrt 2 - 1}}{{\sqrt 2 }}} \right)}} \\\ = \dfrac{{\sqrt 2 }}{4} \\\ = \dfrac{1}{{2\sqrt 2 }} \\\$$

Now, multiply 2 on both the sides, we have,

$$2\sin \theta \cos \theta = \dfrac{2}{{2\sqrt 2 }} \\\ \sin 2\theta = \dfrac{1}{{\sqrt 2 }} \\\ 2\theta = \dfrac{\pi }{4} \\\ \theta = \dfrac{\pi }{8} \\\$$

Thus, the principal argument $\arg \left( {1 + \sqrt 2 + i} \right) = \dfrac{\pi }{8}$.
The option is incorrect as the principal argument is equal to $\dfrac{\pi }{8}$.
Note: The trigonometric identity $2\sin \theta \cos \theta = \sin 2\theta$ is used to simplify the expression. Remember the trigonometric values as here we have used
$\sin A = \dfrac{1}{{\sqrt 2 }}$ giving $A = \dfrac{\pi }{4}$. We have used the Pythagoras theorem in evaluating the value of $\theta$ by finding the value of the side of the right-angled triangle.