Question

Find the power dissipation in resistance $12\Omega$ in the circuit shown above figure.

A. $27W$
B. $20W$
C. $50W$
D. $100W$

Answer 1

In this problem we have to find the power dissipated in resistance $12\Omega$. We will first find the equivalent resistance between $CD$ as they are in series connection. We will then find the equivalent resistance between $AB$. We will then find the power supplied into $12\Omega$ resistance. We will use the fact that voltage across resistance connected in parallel is the same. And voltage across resistance connected in series divides.

Complete step by step answer:
This problem is based on resistance and ohm's law. Resistance is the property of any material through which it opposes the flow of current. It is denoted by symbol $R$. Ohm's law states that the current flowing through a conductor is directly proportional to the voltage across the conductor. Let as draw the given Circuit diagram with the resistance AB and CD is mentioned as follows

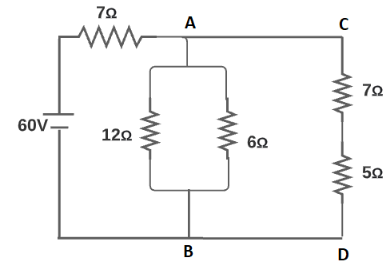
The resistance across $CD$ are in series.
So the equivalent resistance across $CD$ is given as ${R_{CD}} = (7 + 5) = 35\Omega$.
Now the resistance across $AB$ are in parallel.
Therefore equivalent resistance across $AB$ is given by $\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
$\dfrac{1}{{{R_{AB}}}} = \dfrac{1}{{12}} + \dfrac{1}{6} + \dfrac{1}{{12}} = \dfrac{1}{3}$
Hence, ${R_{AB}} = 3$
Given voltage in the circuit = $$$$60V
Voltage between $AB$ = $$$${V_{AB}} = \dfrac{3}{{3 + 7}} \times 60 on solving we have
Hence ${V_{AB}} = 18V$
Hence the voltage across resistor $12\Omega$ is ${V_{AB}} = 18V$
Power dissipated in $12\Omega$ resistance is $P = \dfrac{{{V^2}}}{R}$
Therefore, $\ P = \dfrac{{{{18}^2}}}{{12}} = 27W$
Hence, Power dissipated in $12\Omega$ resistance is $27W$.

Therefore, option $A$ is correct.

Note: Resistance is the property of material, due to which it opposes the flow of current in the circuit. Equivalent resistance in series is given by ${R_{eq}} = {R_1} + {R_2}$. Equivalent resistance in parallel is given by $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$. Voltage across resistance in parallel is the same.Voltage across the resistor in series is different.