Question
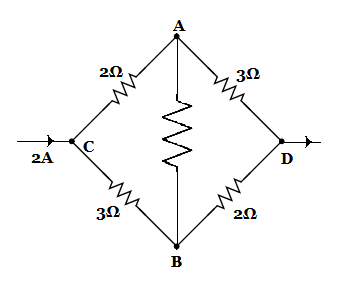
Question: Find the potential difference between points \(A\) and \(B\) i.e. (\({V_A} - {V_B}\)) in the network...
Find the potential difference between points A and B i.e. (VA−VB) in the network shown in figure.
Solution
We shall assume the resistance of the middle resistance as R and the current flowing through it as I. We will also need to assume another current which has been assumed as I1 flowing in the branch CA. The new diagram is as shown below with the currents shown as applicable. Next, we shall apply KVL in the loops ACBA and ADBA to get two equations from which we calculate I.
Complete step by step solution:
The diagram has been redrawn with the currents assumed in the respective branches. All the assumed currents and resistance have been shown in red.
We have assumed the value of the resistance in the branch AB as R. The voltage between the points A and B i.e. (VA−VB) in the network shown will be dependent on the value of the resistance R.
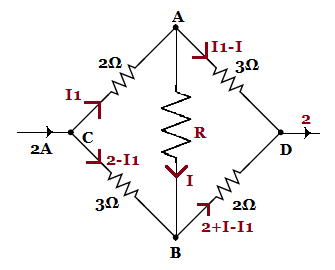
The values of the currents in each branch have been shown. We will apply Kirchhoff's Voltage Law in the loop ACBA and ADBA respectively to get the required values of I1 and I.
After applying Kirchhoff's Voltage Law in the loop ADBA, we will get
IR+2(2+I−I1)=3(I1−I)
⇒IR+4+2I−2I1=3I1−3I
Now on rearranging the terms, we get
⇒IR+5I=5I1−4
⇒I=R+55I1−4
Again applying Kirchhoff's Voltage Law in the loop ABCA, we get
2I1+IR=(2−I1)3
Now substituting the value of I in the above equation, we get
2I1+(R+55I1−4)R=(2−I1)3
⇒(R+5)2I1+R(5I1−4)=(2−I1)3(R+5)
⇒2RI1+10I1+5RI1−4R=6R+30−3I1R−15I1
On rearranging the terms, we get
⇒10RI1+25I1=10R+30
⇒I1=2R+52R+6
Now, substituting this value of I1 in I, we get
I=R+51(2R+510R+30−4)
⇒I=R+51(2R+510R+30−8R−20)
⇒I=R+51(2R+52R+10)
Upon solving further we get
I=2R+52.
Now the voltage drop between the points A and B i.e. (VA−VB) is given by
VA−VB=IR
⇒VA−VB=2R+52R
This is the required potential difference between the two given points.
Thus the required answer is 2R+52RV.
Note:
We have assumed the resistance of the middle resistor, as the voltage drop will be dependent on the resistance of the resistor. This is already shown by the answer found as VA−VB=2R+52R is an equation dependent on the value of the assumed resistance R. We can also see that since the product of the diagonal resistances is not equal in the above bridge-circuit, some current will flow, assumed I.
