Question

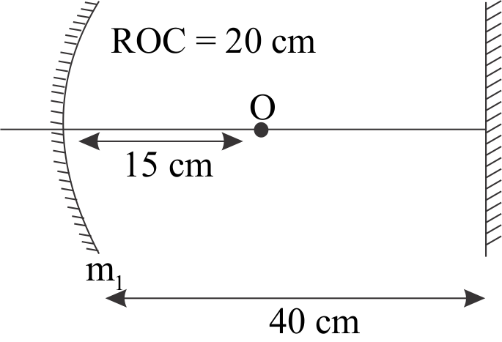
Find the position of the final image after three successive reflections taking the first reflection on ${m_1}$ .

A. $- 12.5{\text{ cm}}$
B. $12.5{\text{ cm}}$
C. $- 30{\text{ cm}}$
D. $30{\text{ cm}}$

Answer 1

The first image will form after being reflected by ${m_1}$ and this image will behave as an object for the plane mirror. Similarly, the image formed by the plane mirror will behave as an object for the mirror ${m_1}$ and the reflection of this object from ${m_1}$ will form the final image.
The position of image by reflection through ${m_1}$ can be found by using mirror formula which is given by $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ where $v$ is the distance of image from the mirror, $u$ is the distance of object from the mirror and $f$ is the focal length of the mirror. The distance of an image formed by a plane mirror is the same as the distance of an object but on the opposite side of the mirror.

Complete step by step answer:
Let us first discuss the image formation on three successive reflections.
The first image will form after being reflected by ${m_1}$ and this image will behave as an object for the plane mirror. Similarly, the image formed by the plane mirror will behave as an object for the mirror ${m_1}$ and the reflection of this object from ${m_1}$ will form the final image.
For first reflection on ${m_1}$, the position of image by reflection through ${m_1}$ can be found by using mirror formula which is given by $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ .
Taking the direction of incident rays to be positive,
$u = - 15{\text{ cm}}$ and $f = - \dfrac{{ROC}}{2} = - 10{\text{ cm}}$
Therefore, using mirror formula we have
$\dfrac{1}{v} + \dfrac{1}{{\left( { - 15} \right)}} = \dfrac{1}{{ - 10}}$
On simplifying we have
$v = - 30{\text{ cm}}$
Now, this image will behave as an object for the plane mirror and we know that the distance of the image formed by a plane mirror is the same as the distance of the object but on the opposite side of the mirror.
For second reflection on plane mirror,
$u = - 10{\text{ cm}}$
Therefore, the image distance $v = 10{\text{ cm}}$ .
Now this image will behave as an object for the mirror ${m_1}$ .
For third reflection on ${m_1}$ ,
$u = - 50{\text{ cm}}$ and $f = - 10{\text{ cm}}$
Therefore, using mirror formula we have
$\dfrac{1}{v} + \dfrac{1}{{\left( { - 50} \right)}} = \dfrac{1}{{ - 10}}$
On simplifying we have
$v = - 12.5{\text{ cm}}$
Therefore, the position of final image will be $v = - 12.5{\text{ cm}}$
Hence, option A is correct.

Note: The mirror ${m_1}$ is a concave mirror which is a converging mirror. The rays of light coming from infinity after being reflected by a concave mirror converge to a point between the pole and centre of curvature of the mirror. This point is called focus of the mirror and the distance from the pole of the mirror and focus is called focal length. The radius of curvature of a spherical mirror is twice the focal length.