Question
Question: Find the position of COM of uniform lamina ABCD (as shown in figure) from O.  from O.
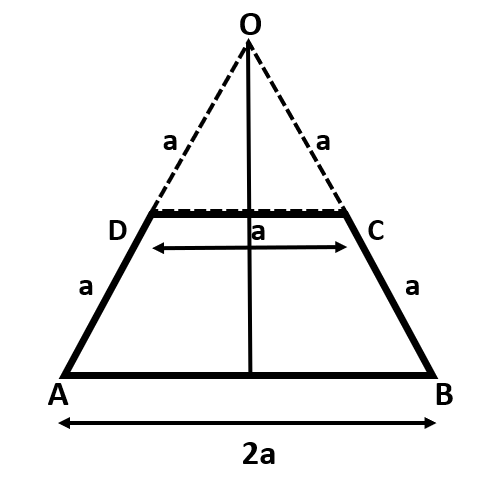
A).23a
B).337a
C).232a
D). None of these
Solution
In order to find the COM of the lamina ABCD, we will consider the triangle OAB to be fully made of the same material as that of lamina ABCD. Then, we can subtract the COM of smaller triangle OCD from the COM of larger triangle OAB, both calculated from O, to get the COM of the lamina ABCD.
Complete step-by-step solution:
First of all we will find what type of triangle is formed by triangle OAB and triangle OCD.
We can see that all the sides of triangle OAB are equal and the length of each side is ‘2a’. Also, in the smaller triangle OCD, the length of all the sides are equal, that is, ‘a’. Thus, both the triangles are equilateral triangles.
Now, from the property of equilateral triangle, we have the COM of an equilateral triangle lies at its centroid which is at a distance of (32h) from any of its vertex,
where ‘h’ is the length of the base.
We can understand this with the help of the following diagram:
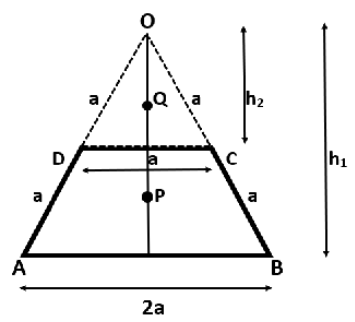
Now, in triangle OAB, we have:
⇒h1=2acos300∴h1=3a
Therefore, its COM from O (say P) is equal to:
⇒P=32h1⇒P=323a
Now, in triangle OCD, we have:
⇒h2=acos300∴h2=23a
Therefore, its COM from O (say Q) is equal to:
⇒Q=32h2⇒Q=3223a⇒Q=33a
Now, the mass of triangle OAB is equal to (assuming surface mass density as d):
⇒MOAB=d×(21×2a×3a)⇒MOAB=3a2d
And, the mass of triangle OCD is equal to:
⇒MOCD=d×(21×a×23a)⇒MOCD=43a2d
Therefore, the COM of lamina ABCD (say X) could be written as:
⇒X=MOAB−MOCDMOABP−MOCDQ
Putting the values of all the terms in the above equation, we get:
⇒X=3a2d−43a2d3a2d×323a−43a2d×33a
On simplifying the above equation, we get:
⇒X=(3−43)(2a−4a)∴X=337a
Hence, the distance of COM of lamina ABCD from the point O comes out to be 337a.
Hence, option (B) is the correct option.
Note: To calculate the COM of lamina only would have been quite tough if we tried to solve it by breaking the lamina into two triangles and one rectangle as it would have taken a lot more calculation and time. In problems like these, we need to find the best possible solution, that is, the one with least amount of time required and least amount of calculation needed.
