Question
Question: Find the position of centre of mass of the uniform planner section shown in figure with respect to t...
Find the position of centre of mass of the uniform planner section shown in figure with respect to the origin (O)
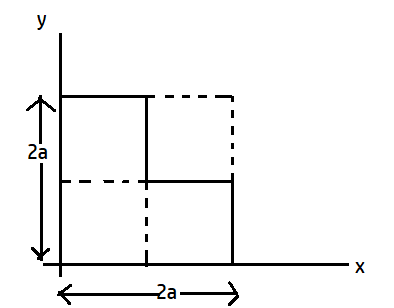
Solution
The centre of mass is a point defined relative to an object or system of objects. It is the aggregate position of all the parts of the system, weighted according to their masses and at this point, it is assumed that the entire mass of the system is contained.
Complete step by step answer: The shape is a square of side 2a and it can be further visualized into 4 smaller squares each of side a. Now, the figure can be divided into 3 smaller segments.
The (x,y) coordinates of the segments can be written as (2a,23a), (2a,2a), (23a,2a)for the first, second and third segment respectively. These are the coordinates that we usually write in geometry and mathematics. Since the mass is equally divided and the total mass of the system is M so the mass of each segment will be 3M
The moment of inertia of a system whose coordinates are given is given as
Xcm=M1+M2+M3M1x1+M2x2+M3x3
Ycm=M1+M2+M3M1y1+M2y2+M3y3
Here there is z coordinate of the system, putting the values we get,
Since the values of M1,M2,M3are equal, we can write it as each segment will be having a mass of M/3
Xcm=M3M(2a+2a+23a)=65a
Ycm=M3M(23a+2a+2a)=65a
So, the coordinates of the centre of mass come out to be (65a′65a)
Note:
For simple rigid objects with uniform density, the centre of mass is located at the geometrical centre, for example, the centre of mass of a ring for example is located at its centre.
