Question

Find the position of centre of mass from the base of a solid hemisphere of radius (A) $16cm$
(B) $4cm$
(C) $6cm$
(D) $8cm$
(E) $12cm$

Answer 1

To solve this question, we need to find out the coordinates of the centre of mass with respect to the base. For this, divide the hemisphere into circular discs and find the centre of mass using integration, taking the origin at the base.
Formula Used: The formula used in this solution is
${r_{com}} = \dfrac{{\int {rdm} }}{{\int {dm} }}$, where $dm$is the mass of the elementary element,$r$is the position of the elementary element, and ${r_{com}}$is the position of the centre of mass.

Complete step-by-step solution
Consider a solid hemisphere of radius$R$, mass$M$, and density $\rho$ as shown in the figure below.

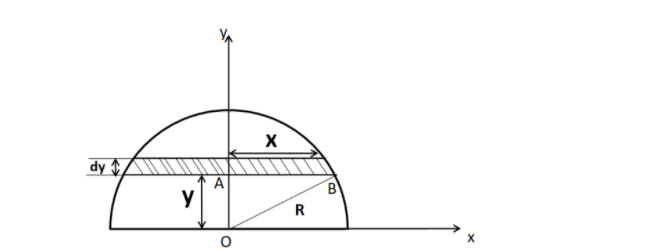
As the hemisphere is symmetrical about the $y$axis, the $x$ coordinate of the centre of mass is$0$, i.e.
${x_{com}} = 0$
As the hemisphere is solid, we divide it into circular discs. Consider an elementary disc of $x$radius at a height $y$ having thickness $dy$ as shown in the figure above.
The mass of the disc $=$Volume of the disc $\times$Density
$dm = \rho dv$ (i)
where$\rho$is the density of the hemisphere and $dv$is the elementary volume of the disc
Now, $\rho = \dfrac{{Mass{\text{ }}of{\text{ }}hemisphere}}{{Volume}}$
We know that Volume of hemisphere, $V = \dfrac{2}{3}\pi {R^3}$
$\therefore \rho = \dfrac{M}{{\dfrac{2}{3}\pi {R^3}}}$
Which gives
$\rho = \dfrac{{3M}}{{2\pi {R^3}}}$ (ii)
Now, Volume of the disc = Area of the disc $\times$ Thickness
$\therefore dv = \pi {x^2}dy$ (iii)
In the triangle $AOB$, by Pythagoras theorem
$O{B^2} = O{A^2} + A{B^2}$
From the figure we have
$OB = R$, $OA = y$ and $AB = x$
$\therefore {R^2} = {y^2} + {x^2}$
Subtracting ${y^2}$from both the sides
${x^2} = {R^2} - {y^2}$
$x = \sqrt {{R^2} - {y^2}}$ (iv)
$\therefore$from (i) we have
$dm = \rho dv$
Substituting $dv$ from (iii)
$dm = \rho (\pi {x^2}dy)$
Substituting $x$ from (iv)
$dm = \rho (\pi ({R^2} - {y^2})dy)$
Now, as we know the $y$ -coordinate of the centre of mass is given by
${r_{com}} = \dfrac{{\int {rdm} }}{{\int {dm} }}$
Substituting $dm = \rho (\pi ({R^2} - {y^2})dy)$
${y_{com}} = \dfrac{{\int {y\rho \pi ({R^2} - {y^2})dy} }}{M}$ (We know that $\int {dm} = M$)
As $y$ varies from $0$ to $R$ in the figure above, we have
${y_{com}} = \dfrac{1}{M}\int\limits_0^R {y\rho \pi ({R^2} - {y^2})dy}$
As $\rho$ and $\pi$ are constants, we can take them out
${y_{com}} = \dfrac{{\rho \pi }}{M}\int\limits_0^R {y({R^2} - {y^2})dy}$
${y_{com}} = \dfrac{{\rho \pi }}{M}\int\limits_0^R {({R^2}y - {y^3})dy}$
Separating into two integrals
${y_{com}} = \dfrac{{\rho \pi }}{M}\left( {\int\limits_0^R {{R^2}ydy - \int\limits_0^R {{y^3}dy} } } \right)$
Taking ${R^2}$ outside as constant
${y_{com}} = \dfrac{{\rho \pi }}{M}\left( {{R^2}\int\limits_0^R {ydy - \int\limits_0^R {{y^3}dy} } } \right)$
Performing integration, we get
${y_{com}} = \dfrac{{\rho \pi }}{M}\left( {{R^2}\left[ {\dfrac{{{y^2}}}{2}} \right]_0^R - \left[ {\dfrac{{{y^4}}}{4}} \right]_0^R} \right)$
Substituting the limits, we have
${y_{com}} = \dfrac{{\rho \pi }}{M}\left( {{R^2}\left[ {\dfrac{{{R^2}}}{2} - \dfrac{{{0^2}}}{2}} \right] - \left[ {\dfrac{{{R^4}}}{4} - \dfrac{{{0^4}}}{4}} \right]} \right)$
${y_{com}} = \dfrac{{\rho \pi }}{M}\left( {\dfrac{{{R^4}}}{2} - \dfrac{{{R^4}}}{4}} \right)$
On simplifying
${y_{com}} = \dfrac{{\rho \pi }}{M}\left( {\dfrac{{{R^4}}}{4}} \right)$
Substituting $\rho$ from (ii), we get
${y_{com}} = \dfrac{{3M}}{{2\pi {R^3}}}\dfrac{\pi }{M}\left( {\dfrac{{{R^4}}}{4}} \right)$
Finally on simplifying, we get
${y_{com}} = \dfrac{{3R}}{8}$
Hence, the $y$ -coordinate of the centre of mass of the hemisphere is $\dfrac{{3R}}{8}$
This $y$ -coordinate is equal to the position of the COM from the base of the hemisphere, as the origin $O$ is taken on the base.
Thus, the position of the centre of mass from the base is given by
$y = \dfrac{{3R}}{8}$
According to the question, $R = 16cm$
Substituting this, we get
$y = \dfrac{{3(16)}}{8}$
$y = 3(2)$
Finally,
$y = 6cm$
So, the position of the centre of mass from the base of the hemisphere is $6cm$

Hence, the correct answer is option B, $6cm$

Note: Always prefer to use as small a number of variables as possible for performing integration. If the number of the variables is more, you may perform the integration incorrectly. To avoid this, convert all the variables in terms of one variable before putting them into the integral.