Question

Find the points on the curve ${{y}^{2}}=2{{x}^{3}}$ at which the slope of the tangent is $3$.

Answer 1

From the given question we have to find the point on the curve ${{y}^{2}}=2{{x}^{3}}$ at which the slope of the tangent is $3$ . Firstly, we have to assume one point and with the help of slope we have to find the relation between $x$ and $y$ then we will get the required point.

Complete step by step solution:
Let us assume $\left( {{x}_{1}},{{y}_{1}} \right)$ is the required point.
Given equation of the curve is
$\Rightarrow {{y}^{2}}=2{{x}^{3}}$
Since $\left( {{x}_{1}},{{y}_{1}} \right)$ lies on the given curve. Therefore, on substituting the point in the given curve equation, we get
$\Rightarrow {{{y}_{1}}^{2}=2{x}_{1}}^{3}$
Let us assume this equation is $\left( 1 \right)$.
Now, differentiate the given curve equation with respect to $x$
By differentiating the curve ${{y}^{2}}=2{{x}^{3}}$ with respect to $x$,we get
$\Rightarrow 2y\dfrac{dy}{dx}=6{x}^{2}$
By shifting $2y$ from left hand side to the right-hand side, we get
$\Rightarrow \dfrac{dy}{dx}=\dfrac{6{{x}^{2}}}{2y}$
$\Rightarrow \dfrac{dy}{dx}=\dfrac{3{{x}^{2}}}{y}$
Now, slope of the tangent at point $\left( {{x}_{1}},{{y}_{1}} \right)={{\left( \dfrac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}=\dfrac{3{{x}_{1}}^{2}}{{{y}_{1}}}$
From the question we also know that the slope of the given equation at the point$\left( {{x}_{1}},{{y}_{1}} \right)$ is $3$.
Therefore,
$\Rightarrow \dfrac{{3{x}_{1}}^{2}}{{{y}_{1}}}=3$
Let us assume the above equation is $\left( 2 \right)$
$\Rightarrow \dfrac{{{x}_{1}}^{2}}{{{y}_{1}}}=1$
$\Rightarrow {{y}_{1}}={{x}_{1}}^{2}$
Now, substitute the value of ${{y}_{1}}$ in the equation $\left( 1 \right)$ , we get
$\Rightarrow {{{y}_{1}}^{2}=2{x}_{1}}^{3}$
$\Rightarrow {{x}_{1}}^{4}=2{{x}_{1}}^{3}$
$\Rightarrow {{x}_{1}}^{4}-2{{x}_{1}}^{3}=0$
$\Rightarrow {{x}_{1}}^{3}\left( {{x}_{1}}-2 \right)=0$
$\Rightarrow {{x}_{1}}=0,2$
Case-$1$
If ${{x}_{1}}=0$ then, by substituting in the equation $\left( 1 \right)$ , we get
$\Rightarrow {{{y}_{1}}^{2}=2{x}_{1}}^{3}$
$\Rightarrow {{y}_{1}}^{2}=2 \times 0$
$\Rightarrow {{y}_{1}}^{{}}=0$
Thus, we got the point $\left( 0,0 \right)$. But this point does not satisfy the equation $\left( 2 \right)$ i.e. $\dfrac{3{{x}_{1}}^{2}}{{{y}_{1}}}=3$
So, we can ignore this point $\left( 0,0 \right)$.
Case-$2$
If ${{x}_{1}}=2$ then, by substituting in the equation $\left( 1 \right)$ , we get
$\Rightarrow {{{y}_{1}}^{2}=2{x}_{1}}^{3}$
$\Rightarrow {{y}_{1}}^{2}=2\times {{\left( 2 \right)}^{3}}$
$\Rightarrow {{y}_{1}}^{2}=2\times 8$
$\Rightarrow {{y}_{1}}^{2}=16$
$\Rightarrow {{y}_{1}}^{{}}=4$
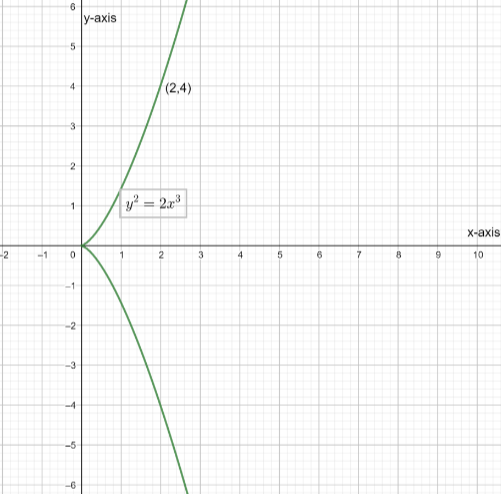
Thus, we get the point $\left( 2,4 \right)$ . This point satisfies the above all equations.
Therefore, the required point is $\left( 2,4 \right)$.
The detail graph for the question will be as follows.

Note: We should have to assume the required point that is the main key step of the given problem. Students should get the idea to assume the point. Remaining steps are based on the formula of slope of a curve and substitution. We must be careful in differentiation for example $\Rightarrow {{y}^{2}}=2{{x}^{3}}$ $\Rightarrow 2y\dfrac{dy}{dx}=6x\dfrac{dy}{dx}$ if do get this it is wrong so Students should be aware of the formulas of slope and differentiation.