Solveeit Logo
Login

Question

Question: Find the point on the ellipse \(4{{x}^{2}}+9{{y}^{2}}=1\) at which tangent is parallel to the line \...

Find the point on the ellipse 4x2+9y2=14{{x}^{2}}+9{{y}^{2}}=1 at which tangent is parallel to the line 8x=9y8x=9y.

Explanation

Solution

In this question we have been given the equation of the ellipse and we have to find the point at which tangent is parallel to a line. We will first find out the slope of the tangent by converting the equation of the line into the general form which is y=mx+cy=mx+c. We will then differentiate the equation of the ellipse and substitute the value of the slope to get the value of xx in terms of yyand then simplify to get the required points on the ellipse.

Complete step by step solution:
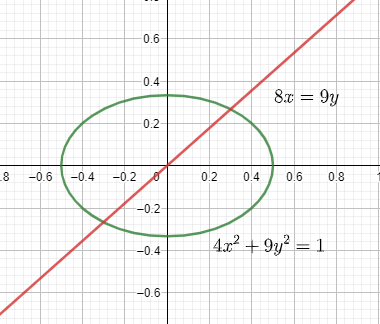
We have the equation of ellipse as 4x2+9y2=14{{x}^{2}}+9{{y}^{2}}=1.
The equation of the line is 8x=9y8x=9y.
We can see the ellipse and the line on the graph as:

Now on rearranging the equation, we get:
⇒9y=8x\Rightarrow 9y=8x
On transferring the term 99 from the left-hand side to the right-hand side, we get:
y=8x9y=\dfrac{8x}{9}
The above equation is in the general form of the equation of line which is y=mx+cy=mx+c given that value of c=0c=0.
We can conclude that the slope is 89\dfrac{8}{9}.
Now to get the value of xx in terms of yy, we will differentiate the equation of ellipse with respect to xx.
On differentiating, we get:
⇒ddx(4x2+9y2=1)\Rightarrow \dfrac{d}{dx}\left( 4{{x}^{2}}+9{{y}^{2}}=1 \right)
We know that ddx(x2)=2x\dfrac{d}{dx}\left( {{x}^{2}} \right)=2x therefore, on using the formula, we get:
⇒4(2x)+9(2ydydx)=1\Rightarrow 4\left( 2x \right)+9\left( 2y\dfrac{dy}{dx} \right)=1
On simplifying, we get:
⇒8x+18ydydx=0\Rightarrow 8x+18y\dfrac{dy}{dx}=0
Now we know that the slope of the line m=dydxm=\dfrac{dy}{dx} therefore, on substituting, we get:
⇒8x+18y(89)=0\Rightarrow 8x+18y\left( \dfrac{8}{9} \right)=0
On simplifying, we get:
⇒8x+16y=0\Rightarrow 8x+16y=0
On dividing both the sides of the expression by 88, we get:
⇒x+2y=0\Rightarrow x+2y=0
On transferring 4y4y from the left-hand side to the right-hand side, we get:
⇒x=−2y\Rightarrow x=-2y
Now we have got the value of xx in terms of yy.
On substituting this value in the equation of ellipse, we get:
⇒4(−2y)2+9y2=1\Rightarrow 4{{\left( -2y \right)}^{2}}+9{{y}^{2}}=1
On squaring, we get:
⇒4(4y2)+9y2=1\Rightarrow 4\left( 4{{y}^{2}} \right)+9{{y}^{2}}=1
On simplifying, we get:
⇒16y2+9y2=1\Rightarrow 16{{y}^{2}}+9{{y}^{2}}=1
On adding the terms, we get:
⇒25y2=1\Rightarrow 25{{y}^{2}}=1
On transferring 2525 from the left-hand side to the right-hand side, we get:
⇒y2=125\Rightarrow {{y}^{2}}=\dfrac{1}{25}
On taking the square root, we get:
⇒y=±15\Rightarrow y=\pm \dfrac{1}{5}
Now we know that x=−2yx=-2y
Therefore, on substituting, we get:
⇒x=−2(±15)\Rightarrow x=-2\left( \pm \dfrac{1}{5} \right)
On simplifying, we get:
⇒x=∓25\Rightarrow x=\mp \dfrac{2}{5}
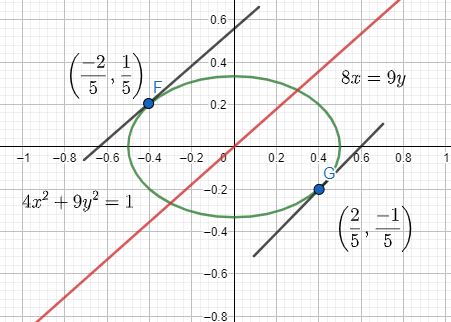
Therefore, the points are (−25,15)\left( \dfrac{-2}{5},\dfrac{1}{5} \right) and (25,−15)\left( \dfrac{2}{5},\dfrac{-1}{5} \right).
From the graph below we can see that the points F=(−25,15)F=\left( \dfrac{-2}{5},\dfrac{1}{5} \right) and G=(25,−15)G=\left( \dfrac{2}{5},\dfrac{-1}{5} \right) are points on the ellipse 4x2+9y2=14{{x}^{2}}+9{{y}^{2}}=1 whose tangents are parallel to the line 8x=9y8x=9y.

Note: It is to be remembered that the slope of the line refers to the inclination of the line. It tells us the steepness of the line. It is also called the gradient. It is to be remembered that the general equation of an ellipse is x2a2+y2b2=1\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1, where aa represents half the length of the major axis and bb represents half the length of the minor axis.