Solveeit Logo
Login

Question

Question: Find the point of intersection of y-axis and the perpendicular bisector of \((2, - 3)\) and \(( - 4,...

Find the point of intersection of y-axis and the perpendicular bisector of (2,−3)(2, - 3) and (−4,1)( - 4,1).

Explanation

Solution

As in this question first try to find out the midpoint of points (2,−3)(2, - 3) and (−4,1)( - 4,1) then for the slope as we know that m1.m2=−1{m_1}.{m_2} = - 1 if line is perpendicular hence one slope we know other will find out then find out the equation of line perpendicular to it and at last find the intersection with y-axis

Complete step-by-step answer:
As in the given question first we have to find the equation of perpendicular bisector of points (2,−3)(2, - 3) and (−4,1)( - 4,1)
Perpendicular bisector means line passing through midpoint and perpendicular to the point (2,−3)(2, - 3) and (−4,1)( - 4,1)

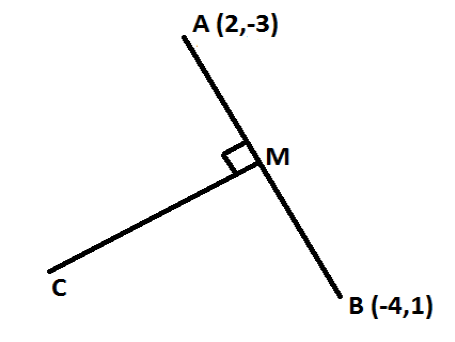
Hence the midpoint of point (2,−3)(2, - 3) and (−4,1)( - 4,1) is M equal to
x=x1+x22x = \dfrac{{{x_1} + {x_2}}}{2} and y=y1+y22y = \dfrac{{{y_1} + {y_2}}}{2}
or
x=2+(−4)2x = \dfrac{{2 + ( - 4)}}{2} and y=−3+12y = \dfrac{{ - 3 + 1}}{2}
x=−1x = - 1 and y=−1y = - 1
Hence the midpoint of A (2,−3)(2, - 3) and B (−4,1)( - 4,1) is M (−1,−1)( - 1, - 1)
Now for the equation of line we need the slope of the line , As we know that the line MC is perpendicular to the line AB joining point (2,−3)(2, - 3) and (−4,1)( - 4,1)
Hence we know that m1.m2=−1{m_1}.{m_2} = - 1
means Slope of line AB ×\times Slope of MC = −1 - 1
Slope of AB equal to = m1{m_1} = y2−y1x2−x1\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}
= 1−(−3)−4−2\dfrac{{1 - ( - 3)}}{{ - 4 - 2}}
= 1+3−4−2\dfrac{{1 + 3}}{{ - 4 - 2}}
= 4−6\dfrac{4}{{ - 6}}
m1{m_1} = −23 - \dfrac{2}{3}
Slope of MC = m2{m_2}
Hence for m2=−1m1{m_2} = -\dfrac{1}{{{m_1}}}= 1−23\dfrac{1}{{ - \dfrac{2}{3}}}
m2=32{m_2} = \dfrac{3}{2}
Equation of line MC is whose one point is (−1,−1)( - 1, - 1) and slope is m2=32{m_2} = \dfrac{3}{2}
(y−y1)=m2(x−x1)(y - {y_1}) = {m_2}(x - {x_1})
(y+1)=−32(x+1)(y + 1) = -\dfrac{3}{2}(x + 1)
In the question we have to find the point of intersection of this line with the y-axis .
For the y-axis X=0X = 0 ,put it in the equation of line MC
(y+1)=32(0+1)(y + 1) = \dfrac{3}{2}(0 + 1)
y+1=32y + 1 = \dfrac{3}{2}
y=32−1y = \dfrac{3}{2} - 1
y=12y = \dfrac{1}{2}
Hence the point of intersection of y-axis and the perpendicular bisector of (2,−3)(2, - 3) and (−4,1)( - 4,1) is (0,12)\left( {0, \dfrac{1}{2}} \right)

Note: As in the question we use for the midpoint of line AB is x=x1+x22x = \dfrac{{{x_1} + {x_2}}}{2} and y=y1+y22y = \dfrac{{{y_1} + {y_2}}}{2}
this is nothing but the section formula x=mx1+nx2m+nx = \dfrac{{m{x_1} + n{x_2}}}{{m + n}} or y=my1+ny2m+ny = \dfrac{{m{y_1} + n{y_2}}}{{m + n}} which have m=1,n=1m = 1,n = 1 because we have to find midpoint M hence M divides line AB in equal ratio .
For finding the equation of line we need one point and the slope of that line as in this question we find a point as midpoint M and the slope with formula m1.m2=−1{m_1}.{m_2} = - 1