Question

Find the period and amplitude of the following functions.
$\begin{aligned} & a)y=\sin 7x \\\ & b)y=-\sin \left( \dfrac{1}{3}x \right) \\\ & c)y=4\sin \left( -2x \right) \\\ \end{aligned}$

Answer 1

Now for a trigonometric function in the form of $a\sin \left( bx+c \right)$. Amplitude is given by |a|. Time period is given by formula $\dfrac{2\pi }{|b|}$ . Hence we will use this to find amplitude and period of the given functions.

Complete step-by-step solution:
Now let us first understand the Amplitude and time period.
The amplitude of the function is nothing but the distance between the center line and the top of the function or centerline and the bottom of the function. Hence amplitude is the height of function from the center.
For the function sin x. we have amplitude is 1.

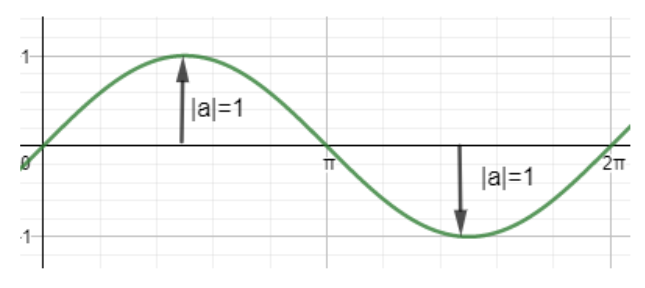
Now let us understand what time period is.
The time period is the distance between two peaks. This is nothing but the period after which a function repeats itself. A function is periodic if it repeats the same value after a period. A function f (x) is called periodic with period T if $f(x + T) = f(x).$
Now consider sin x. for this function we have period $2\pi$as it repeats the same values after $2\pi$

Now if we have function of the form $a\sin \left( bx+c \right)$ then the period of the function is given by $\dfrac{2\pi }{|b|}$ and amplitude of the function is given by |a|
Now let us consider the first option
The given function is $\sin7x$.
By comparing the given function with $a\sin \left( bx+c \right)$ we get $a = 1, b = 7$ and $c = 0.$
Hence the amplitude is $|a| = |1| = 1.$
And time period is $\dfrac{2\pi }{|b|}=\dfrac{2\pi }{7}$ .
Now consider the second option
The given function is $-\sin \left( -\dfrac{1}{3} \right)$.
By comparing the given function with $a\sin \left( bx+c \right)$ we get a = $-1$ , b = $-\dfrac{1}{3}$ and $c = 0.$
Hence the amplitude is $|a| = |–1| = 1.$
And time period is $\dfrac{2\pi }{\left| \dfrac{-1}{3} \right|}=6\pi$ .
Now consider the last option
The given function is $4 \sin(–2x).$
By comparing the given function with $a\sin \left( bx+c \right)$ we get $a = 4, b = -2$ and $c = 0.$
Hence the amplitude is $|a| = |4| = 4.$
And time period is $\dfrac{2\pi }{|b|}=\dfrac{2\pi }{2}=\pi$ .

Note: Now note that when we have function of the form sin(ax), then the time period decreases if $a > 1$ and increases if $a < 1$. Note that we can also find phase shift for the function $a\sin \left( bx+c \right)$ . and the phase shift is given by $\dfrac{c}{b}$ . Phase shift shows how much the function is shifted horizontally.