Question

Find the percentage decrease in Acceleration due to gravity $\left( {{g}} \right)$. When a body is taken from the surface of Earth to a height of $64{{km}}$ from its surface $\left[ {{{Re = 6}}{{.4 \times 1}}{{{0}}^{{6}}}{{metre}}} \right]$

Answer 1

The acceleration of a body in free fall is called acceleration due to gravity. It is denoted by $'{{g}}'$. Its value is $9.8\dfrac{{{m}}}{{{{\sec }^2}}}$ maximum on the surface of the earth. The Value of Acceleration due to gravity will decrease with the increase in height from the surface of the earth. Here we will consider the Radius of Earth is $6400{{km}}$.

Formula used:-
Here we will use the formula
${{g' = g}}\left( {1 - \dfrac{{2{{h}}}}{{{R}}}} \right)$
Where ${{g'}}$ is the value of acceleration due to gravity at a particular height
${{g}}$ is the acceleration due to gravity on the surface of Earth.
${{R = }}$ the radius of Earth.
${{'h' = }}$ height above from the surface of Earth.

Complete Step by step solution:
Here as shown in the figure$\left( {1.01} \right)$ Earth’s spherical shape of Centre ${{O}}{{.}}$ and radius ${{Re}}{{.}}$ where ${{'M'}}$ is the mass of Earth.

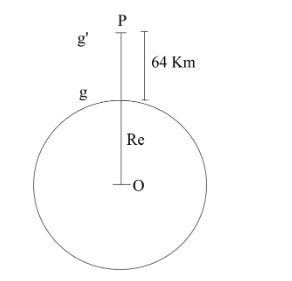
The value of acceleration due to gravity is ${{'g'}}$ at S. and ${{g'}}$ at point P. Which we have to calculate now the formula we have.
${{g' = g}}\left( {{{1 - }}\dfrac{{{{2h}}}}{{{R}}}} \right)$
Also
$\dfrac{{{{g'}}}}{{{g}}}{{ = }}\left( {{{1 - }}\dfrac{{{{2h}}}}{{{{Re}}}}} \right)$ $- \left( 1 \right)$
Where ${{h = 64km}}$
${{Re = 6400}}$
Now put the values of ${{'h'}}$
And in ${{R}}$in equation $\left( 1 \right)$
$\dfrac{{{{g'}}}}{{{g}}}{{ = 1 - }}\dfrac{{{{2 \times 64}}}}{{{{6400}}}}{{ = 1 - }}\dfrac{{{{128}}}}{{{{6400}}}}$
Now adding $\left( { - 1} \right)$ on the both the sides
${{ - 1 + }}\dfrac{{{{g'}}}}{{{g}}}{{ = - 1 + 1 - }}\dfrac{{{{128}}}}{{{{6400}}}}$
Now taking the common negative sign from both sides and then cancels it.
${{1 - }}\dfrac{{{{g'}}}}{{{g}}}{{ = X - X + }}\dfrac{{{{128}}}}{{{{6400}}}}$
$\dfrac{{{{g - g'}}}}{{{g}}}{{ = }}\dfrac{{{{128}}}}{{{{6400}}}}$
Now for the percentage change
$\dfrac{{{{g - g'}}}}{{{g}}}{{ \times 100 = }}\dfrac{{{{128}}}}{{{{6400}}}}{{ \times 100 = 2\% }}$

Hence the value of acceleration due to gravity is decreased by $2\%$ at P.

Additional Information:
-The Value of acceleration due to gravity also depends upon the shape of the earth. It is maximum at the poles and minimum as the equator.
-It does not depend upon the shape and size of the body. It depends upon the following factors.
${{{g}}_{{p}}}{{ = }}\dfrac{{{{G}}{{{M}}_{{p}}}}}{{{{R}}_{{p}}^{{2}}}}$
${{M = }}$ mass of the planet.
${{G = }}$ Gravitational constant
${{R = }}$ Radius of the planet.
-It will be zero at the Centre of earth.
-The Value of ${{g}}$ at the moon is $\dfrac{1}{6}$ times of its value on the surface of the earth.

Note: While calculating the solution from this question, we should be very cautious about the formulae. Also, we should always remember that gravity always decreases as we go away from the earth surface. The same thing happens with acceleration as we move towards the earth centre.