Question

Find the peak current and resonant frequency of the following circuit (as shown in figure)

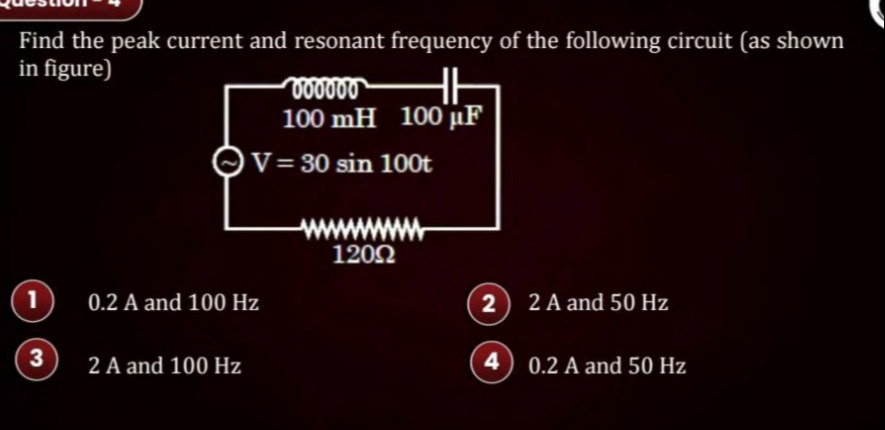
• A. 0.2 A and 100 Hz
• B. 2 A and 50 Hz
• C. 2 A and 100 Hz
• D. 0.2 A and 50 Hz

Answer 1

Answer: (D)

0.2 A and 50 Hz

Answer 2

The AC voltage source is given by $V(t) = 30 \sin(100t)$, so the peak voltage is $V_0 = 30$ V and the angular frequency is $\omega = 100$ rad/s. The components are $R = 120 \, \Omega$, $L = 100$ mH $= 0.1$ H, and $C = 100 \, \mu\text{F} = 10^{-4}$ F.

The inductive reactance is $X_L = \omega L = 100 \times 0.1 = 10 \, \Omega$. The capacitive reactance is $X_C = \frac{1}{\omega C} = \frac{1}{100 \times 10^{-4}} = \frac{1}{10^{-2}} = 100 \, \Omega$. The impedance of the circuit is $Z = \sqrt{R^2 + (X_L - X_C)^2} = \sqrt{120^2 + (10 - 100)^2} = \sqrt{14400 + (-90)^2} = \sqrt{14400 + 8100} = \sqrt{22500} = 150 \, \Omega$. The peak current is $I_0 = \frac{V_0}{Z} = \frac{30 \, \text{V}}{150 \, \Omega} = 0.2 \, \text{A}$.

The resonant angular frequency $\omega_0$ is given by $\omega_0 = \frac{1}{\sqrt{LC}}$. The resonant frequency in Hertz is $f_0 = \frac{\omega_0}{2\pi} = \frac{1}{2\pi\sqrt{LC}}$. Substituting the values of $L$ and $C$: $f_0 = \frac{1}{2\pi\sqrt{(0.1 \, \text{H}) \times (10^{-4} \, \text{F})}} = \frac{1}{2\pi\sqrt{10^{-5}}} \approx \frac{1}{2\pi \times 0.003162} \approx \frac{1}{0.01986} \approx 50.35$ Hz. This is approximately 50 Hz.

Therefore, the peak current is 0.2 A and the resonant frequency is approximately 50 Hz.