Question

Find the number of the common tangents to the circle ${{x}^{2}}+{{y}^{2}}-4x-6y-12=0$ and ${{x}^{2}}+{{y}^{2}}+6x+18y+26=0$.

Answer 1

Hint: Write down the conditions for getting common tangents. Take ${{C}_{1}}$ and ${{C}_{2}}$ as the center of the circle and ${{r}_{1}}$ and ${{r}_{2}}$ as the radius. From the 2 given equations for the center and radius of the circle, find ${{C}_{1}}{{C}_{2}}$ using distance formula and $\left( {{r}_{1}}+{{r}_{2}} \right)$. Compare their value with the conditions.

Complete step-by-step answer:
We have been given the equation of two circles. Let us call the circles as ${{C}_{1}}$ and ${{C}_{2}}$. Now both these circles have a common tangent. Take the radius of both circles as ${{r}_{1}}$ and ${{r}_{2}}$.
Now we don’t know where the common tangent meets. Let us look into some conditions of how common tangents can be formed.
(i) When one circle lies completely inside the other without touching then there are no common tangents: - ${{C}_{1}}{{C}_{2}}<\left| {{r}_{1}}-{{r}_{2}} \right|$.
(ii) When 2 two circles touch each other internally, then 1 common tangent. i.e. $\left| {{r}_{1}}-{{r}_{2}} \right|={{C}_{1}}{{C}_{2}}$.
(iii) When 2 circles intersect in two real and distinct points, 2 common tangents can be drawn to the circle. i.e. $\left| {{r}_{1}}-{{r}_{2}} \right|<{{C}_{1}}{{C}_{2}}<{{r}_{1}}+{{r}_{2}}$.
(iv) When 2 circles touch each other externally, 3 common tangents. ${{r}_{1}}+{{r}_{2}}={{C}_{1}}{{C}_{2}}$.
(v) When 2 circles neither touch nor intersect and one lies outside the other, then 4 common tangents. i.e. ${{r}_{1}}+{{r}_{2}}<{{C}_{1}}{{C}_{2}}$.

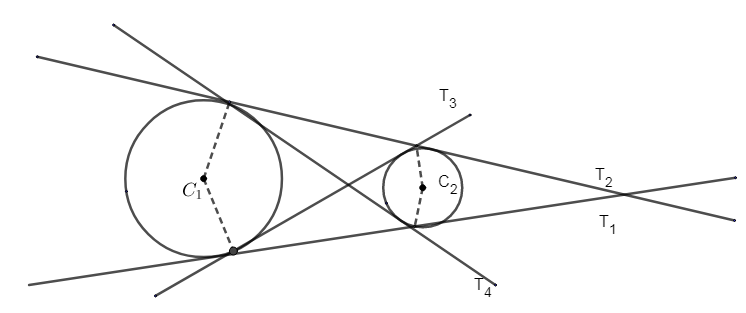
From the figure ${{T}_{3}}$ and ${{T}_{4}}$ represent the internal common tangent.
${{T}_{2}}$ and ${{T}_{1}}$ represent the external common tangent.
Now given to us the equation of circle,

& {{x}^{2}}+{{y}^{2}}-4x-6y-12=0-(1) \\\ & {{x}^{2}}+{{y}^{2}}+6x+18y+26=0-(2) \\\ \end{aligned}$$ Now, the general equation of a circle is of the form, $${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}-(3)$$, where (h, k) is the center and r is the radius. Now, let us find the center and radius of both circles. From (1) $$\Rightarrow {{x}^{2}}-4x+{{y}^{2}}-6y-12=0$$ Now add and subtract $${{2}^{2}}$$ and $${{3}^{2}}$$ in the above expression. $$\begin{aligned} & {{x}^{2}}-4x+{{2}^{2}}+{{y}^{2}}-6y+{{3}^{2}}-12-{{2}^{2}}-{{3}^{2}}=0 \\\ & {{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=12+4+9 \\\ \end{aligned}$$ $${{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=25$$, Now this is of the form of equation (3). Thus, center of circle 1 = (h, k) = (2, 3). Radius, $${{r}_{1}}=\sqrt{25}=5$$. Thus for a circle, $${{C}_{1}}$$: - center (2, 3) and $${{r}_{1}}=5$$. Similarly, let us find the center and radius of circle 2. From (2), $${{x}^{2}}+6x+{{y}^{2}}+18y+26=0$$. Add and subtract $${{3}^{2}}$$ and $${{9}^{2}}$$ from the above expression. $$\begin{aligned} & {{x}^{2}}+6x+{{3}^{2}}+{{y}^{2}}+18y+{{9}^{2}}+26-{{3}^{2}}-{{9}^{2}}=0 \\\ & {{\left( x+3 \right)}^{2}}+{{\left( y+9 \right)}^{2}}=81+9-26 \\\ \end{aligned}$$ $${{\left( x+3 \right)}^{2}}+{{\left( y+9 \right)}^{2}}=64$$, Now this is of the form of equation (3). $$\therefore $$ Center of circle 2, $${{C}_{2}}=\left( h,k \right)=\left( -3,-9 \right)$$. Radius, $${{r}_{2}}=\sqrt{64}=8$$. Hence, radius of circle 2, $${{r}_{2}}$$ = 8cm and center = (-3, -9). Now, we have, $${{C}_{1}}=\left( 2,3 \right),{{C}_{2}}=\left( -3,-9 \right)$$. $${{r}_{1}}=5,{{r}_{2}}=8$$ Now let us compare $${{C}_{1}}{{C}_{2}}$$ and $$\left( {{r}_{1}}+{{r}_{2}} \right)$$. $${{C}_{1}}{{C}_{2}}$$ can be found using the distance formula, Distance formula $$=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$$ $$\begin{aligned} & {{C}_{1}}=\left( 2,3 \right)=\left( {{x}_{1}},{{y}_{1}} \right) \\\ & {{C}_{2}}=\left( -3,-9 \right)=\left( {{x}_{2}},{{y}_{2}} \right) \\\ & \therefore {{C}_{1}}{{C}_{2}}=\sqrt{{{\left( -3-2 \right)}^{2}}+{{\left( -9-3 \right)}^{2}}}=\sqrt{{{\left( -5 \right)}^{2}}+{{\left( -12 \right)}^{2}}} \\\ & \therefore {{C}_{1}}{{C}_{2}}=\sqrt{25+144}=\sqrt{169}=13 \\\ & \therefore {{C}_{1}}{{C}_{2}}=13 \\\ & {{r}_{1}}+{{r}_{2}}=5+8=13 \\\ \end{aligned}$$ i.e. $${{C}_{1}}{{C}_{2}}={{r}_{1}}+{{r}_{2}}$$, now let us compare this with the conditions given. From (iii), the circle will touch each other externally. Hence, there are 3 common tangents, as the circles of the two externally. Note: The distance between the centers of the two circles are equal to the sum of radii of the circle to keep a possibility of direct common tangents, which is clear from the figure we have drawn. The transverse or direct common tangents always meet on the line joining centers of the two circles.