Question

Find the number of solutions of the equation $2{{\cos }^{-1}}x-x-3=0$
[a] No solution
[b] One solution
[c] Two solutions
[d] More than two solutions

Answer 1

- Hint: Draw the graphs of ${{\cos }^{-1}}x$ and x+3 and find the number of points of intersection of these curves. The number of points at which these curves intersect gives the number of solutions of the given equation.

Complete step-by-step solution -

Before dwelling into the solution of the above question, we must understand how ${{\cos }^{-1}}x$ is defined even when $\cos x$ is not one-one.
We know that cosx is a periodic function.
Let us draw the graph of cosx

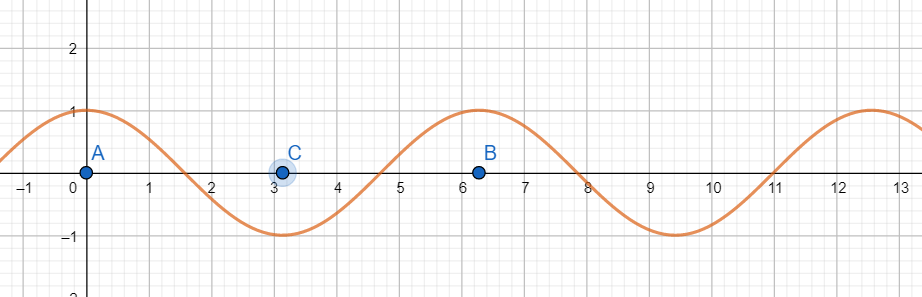
As is evident from the graph cosx is a repeated chunk of the graph of cosx within the interval [A, B] and it attains all its possible values in the interval [A, C]. Here $A=0,B=2\pi$ and $C=\pi$.
Hence if we consider cosx in the interval [A, C], we will lose no value attained by cosx, and at the same time, cosx will be one-one and onto.
Hence ${{\cos }^{-1}}x$ is defined over the domain $\left[ -1,1 \right]$, with codomain $\left[ 0,\pi \right]$ as in the domain $\left[ 0,\pi \right]$, cosx is one-one and ${{R}_{\cos x}}=\left[ -1,1 \right]$.
At the point of solution, we have
$2{{\cos }^{-1}}x=x+3$.
Hence we plot the graphs of $2{{\cos }^{-1}}x$ and x+3 and find the number of intersection points of these curves. This will give the number of solutions of the equation.

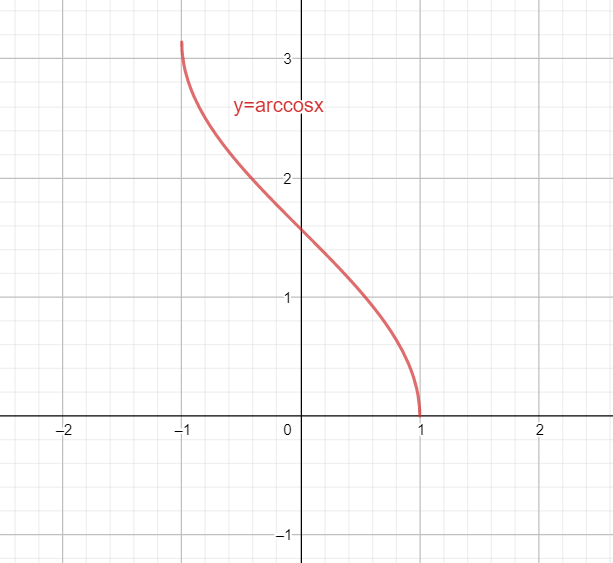
The graph of an inverse of a function is the mirror image of the function with respect to the line y=x.
Hence the graph of ${{\cos }^{-1}}x$ is as follow

If the graph of f(x) is known, then the graph of af(x) can be drawn by extending the graph “a” times along the y-axis.
Hence the graph of $2{{\cos }^{-1}}x$ can be plotted as shown below

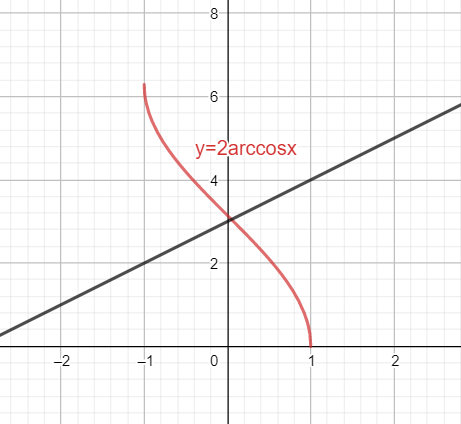
The graph of x+3 is a straight line passing through (-3,0) and (0,3)
Hence the graph of x+3 can be plotted as shown below

As is evident from the graph, the two graphs intersect at one point. Hence the number of solutions of the equation is one.
Hence option [b] is correct.

Note: [1] Alternative Solution:
A strictly increasing and a strictly decreasing continuous function can cut each other at most one point.
We know that $2{{\cos }^{-1}}x$ is a strictly decreasing continuous function and $x+3$ is a strictly increasing continuous function. Hence the number of solutions can be at most one.
Now at x= -1, we have $2{{\cos }^{-1}}\left( -1 \right)=2\pi$ and $-1+3=2$
Hence $2{{\cos }^{-1}}x$ lies above x+3
At x= 1, we have $2{{\cos }^{-1}}1=0$ and $1+3=4$
Hence $2{{\cos }^{-1}}x$ lies below x+3.
Hence in between the domain [-1,1], the two functions cut each other.
Hence the number of solutions is exactly one.