Question

Find the number of solution for the equation $\sin x=-4x+1$

Answer 1

To find the number of solution/s, we form a graphical representation of $\sin x$ and $-4x+1$ separately. After drawing them we check where the two graphs intersect, and how many times they intersect and mark those points of intersection as those points of intersection are the valuation for the total number of solutions for the equation $\sin x=-4x+1$.

Complete step-by-step answer:
First, we draw the graph for $\sin x$ (in red) to check the domain and range and the graphical representation over the $x,y$ axis.

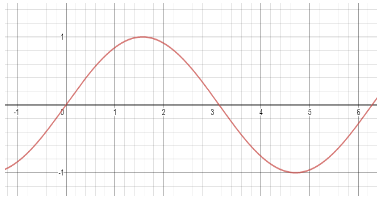
The graph has a domain of all real numbers till infinity and the range stretches from $\left[ -1,1 \right]$.
For $-4x+1$ (in blue), we again draw a graph to check the domain and range and the graphical representation over $x,y$ axis.

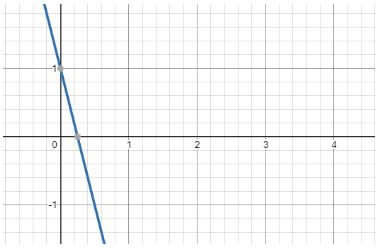
The graph has a domain of all real numbers till infinity and the range also has real numbers till infinity.
Now let us put both the graphs together:

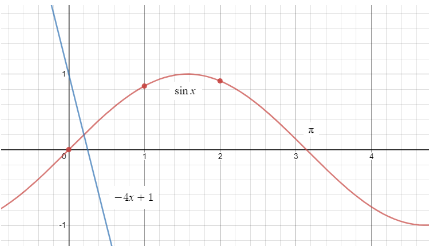
After drawing the graph we can see that there is only one point of contact between the graphs as the domain of $\sin x$ is all real numbers and range is $\left[ -1,1 \right]$ whereas for $-4x+1$ the domain and range are all real numbers. Hence, there is only one point of contact i.e. in between $\left[ -1,1 \right]$ making the total number of solutions equal to one.

Note: The elaborate way to explain the point of intersection is by finding the domain and range of both L.H.S and R.H.S.. The domain and range for R.H.S. is Domain: \left( -\infty ,\infty \right),\left\\{ x\left| x\in R \right. \right\\} and the domain for L.H.S is Domain: \left( -\infty ,\infty \right),\left\\{ x\left| x\in R \right. \right\\} and for range it is Range: \left[ -1,1 \right],\left\\{ \left. y \right|-1\le y\le 1 \right\\}. Now in terms of domain both of them are the same hence, the possibility of intersection is only possible in between \left[ -1,1 \right],\left\\{ \left. y \right|-1\le y\le 1 \right\\} which is the range of L.H.S.