Question

Find the number of roots of ${{\cos }^{7}}x+{{\sin }^{4}}x=1$ in the interval $\left[ -\pi ,\pi \right]$.

Answer 1

We have to convert the equation into the same trigonometric function for taking factorisation. We change $\sin x$ into $\cos x$ to form a factorisation. Then we solve the equation to find the roots individually. We take help of a graph to find the points in the interval $\left[ -\pi ,\pi \right]$.

Complete step-by-step answer:
We need to break the given trigonometric equation. The main requirement would be reducing the power and form the factorisation.
We know that ${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$.
So, $1-{{\sin }^{4}}x={{1}^{2}}-{{\left( {{\sin }^{2}}x \right)}^{2}}=\left( 1+{{\sin }^{2}}x \right)\left( 1-{{\sin }^{2}}x \right)={{\cos }^{2}}x\left( 1+{{\sin }^{2}}x \right)$
Now we have been given ${{\cos }^{7}}x+{{\sin }^{4}}x=1$
Changing sides, we get ${{\cos }^{7}}x=1-{{\sin }^{4}}x={{\cos }^{2}}x\left( 1+{{\sin }^{2}}x \right)$
Now we take all on the same side to form factorisation
$\begin{aligned} & {{\cos }^{7}}x={{\cos }^{2}}x\left( 1+{{\sin }^{2}}x \right) \\\ & \Rightarrow {{\cos }^{7}}x-{{\cos }^{2}}x\left( 1+{{\sin }^{2}}x \right)=0 \\\ & \Rightarrow {{\cos }^{2}}x\left( {{\cos }^{5}}x-1-{{\sin }^{2}}x \right)=0 \\\ \end{aligned}$
The multiplication of two terms is 0 which means at least one of them has to be 0. We also have been given the interval $\left[ -\pi ,\pi \right]$.
So, let’s assume ${{\cos }^{2}}x=0$ which means $\cos x=0$.
It means in the interval $\left[ -\pi ,\pi \right]$ the points x for which $\cos x=0$ is $x=\pm \dfrac{\pi }{2}$.
The other part will be $\left( {{\cos }^{5}}x-1-{{\sin }^{2}}x \right)$.
We try to make the equation in the form of $\cos x$ only.
So, $\left( {{\cos }^{5}}x-1-{{\sin }^{2}}x \right)={{\cos }^{5}}x-1-\left( 1-{{\cos }^{2}}x \right)={{\cos }^{5}}x-2+{{\cos }^{2}}x$.
We can see the graph of the equation.

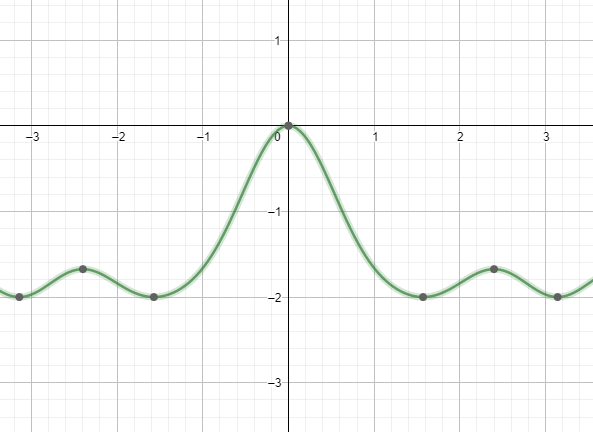
In the interval the only solution for the equation is $x=0$.
So, in total there are there solutions of the equation ${{\cos }^{7}}x+{{\sin }^{4}}x=1$ in the interval $\left[ -\pi ,\pi \right]$.
Those are $x=\pm \dfrac{\pi }{2},0$. So, there are three roots.

Note: We don’t need to simplify the last equation as the range of the function is crucial. Also, we can take help of differentiation to find the solution of the second equation. For trigonometric equations it’s always better to make the equation change from $\sin x$ into $\cos x$ as the latter one is an even function. It causes less error in finding roots.