Question

Find the number of points with integral coordinates that lie in the interior of the region common to circle ${x^2} + {y^2} = 16$ and the parabola ${y^2} = 4x.$
A.8
B.10
C.16
D.None of these

Answer 1

Hint: We need to imagine the graphs of circle and parabola and the intersection of those two figures in a graph.
Let $\left( {\alpha ,\beta } \right)$ be the point with integral coordinates and lying in the interior of the region common to the circle ${x^2} + {y^2} = 16$ and the parabola ${y^2} = 4x.$
Then ${\alpha ^2} + {\beta ^2} - 16 < 0$ and ${\beta ^2} - 4\alpha < 0$

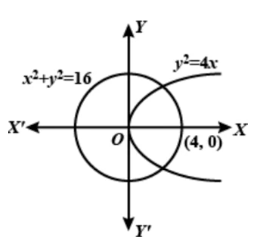
It is clear from the figure that $0 < \alpha < 4$ .
$\Rightarrow \alpha = 1,2,3$ $\left[ {\because \alpha \in Z} \right]$
When $\alpha = 1$
${\beta ^2} < 4\alpha$
$\Rightarrow {\beta ^2} < 4$
$\Rightarrow \beta = 0,1$
So the points are (1, 0) and (1, 1).
When $\alpha = 2$
${\beta ^2} < 4\alpha$
$\Rightarrow {\beta ^2} < 8$
$\Rightarrow \beta = 0,1,2$
So the points are (2, 0), (2, 1) and (2, 2).
When $\alpha = 3$
${\beta ^2} < 4\alpha$
$\Rightarrow {\beta ^2} < 12$
$\Rightarrow \beta = 0,1,2,3$
So the points are (3, 0), (3, 1), (3, 2) and (3, 3)
Out of these four points (3, 3) does not satisfy ${\alpha ^2} + {\beta ^2} - 16 < 0$.
Thus, the points lying in the region are (1, 0), (1, 1), (2, 0), (2, 1), (2, 2), (3, 0), (3, 1) and (3, 2).
Note:
It is always better to start with the graph of given equations for these kinds of problems for better visualization.