Question

Find the number of planes of symmetry in ${\text{CC}}{{\text{l}}_{\text{4}}}$ molecule:
A. $6$
B. $5$
C. $7$
D. $4$

Answer 1

To answer we should know what the plane of symmetry is and how to find it. We will draw the geometry of the molecule first. So, we understand the planes present in it. After drawing the geometry of the molecule we will find the plane which dissects the molecule in two equal half parts.

Complete solution: The plane which bisects the molecule as such that the bisected parts are the mirror image of each other is known as a plane of symmetry.
As symmetry means that two parts are the same, when the two parts become equal or we can say the same by passing a plane then the plane is known as a plane of symmetry.
The geometry of a molecule is tetrahedral which is shown as follow:

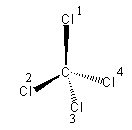
(all the chlorine atoms are the same. Just for better understanding, we have given the numbering).
The chlorine atoms that are on the wedge line are towards us and the chlorine present on the dashed line are away from us.
Assume a cube, then consider its two faces above one and below one. Each has four corners. Now place two atoms (chlorine) at the alternate corner of each face and an atom (carbon) in between the
Cube. The geometry obtained by this arrangement is known as tetrahedral that is shown as below:

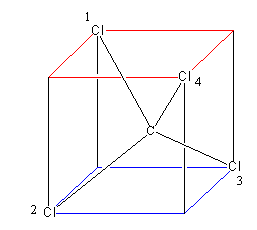
Now let’s pass a plane, from the chlorine$1$ and chlorine $2$, which will bisect the chlorine$1$ and chlorine $2$, and pass through chlorine$3$ and chlorine $4$.
Similarly we can pass a second plane from chlorine$1$ and chlorine$3$,$2$, which will bisect the chlorine$1$ and chlorine $3$, and pass through chlorine$2$ and chlorine $4$.
So, tetrahedral has a total of six planes that are shown as follows:
Plane Bisecting Passing
$1$ ${\text{C}}{{\text{l}}_{\text{1}}} - {\text{C}}{{\text{l}}_{\text{2}}}$ ${\text{C}}{{\text{l}}_3} - {\text{C}}{{\text{l}}_4}$
$2$ ${\text{C}}{{\text{l}}_{\text{1}}} - {\text{C}}{{\text{l}}_3}$ ${\text{C}}{{\text{l}}_2} - {\text{C}}{{\text{l}}_4}$
$3$ ${\text{C}}{{\text{l}}_{\text{1}}} - {\text{C}}{{\text{l}}_4}$ ${\text{C}}{{\text{l}}_2} - {\text{C}}{{\text{l}}_3}$
$4$ ${\text{C}}{{\text{l}}_2} - {\text{C}}{{\text{l}}_3}$ ${\text{C}}{{\text{l}}_{\text{1}}} - {\text{C}}{{\text{l}}_4}$
$5$ ${\text{C}}{{\text{l}}_2} - {\text{C}}{{\text{l}}_4}$ ${\text{C}}{{\text{l}}_{\text{1}}} - {\text{C}}{{\text{l}}_3}$
$6$ ${\text{C}}{{\text{l}}_3} - {\text{C}}{{\text{l}}_4}$ ${\text{C}}{{\text{l}}_{\text{1}}} - {\text{C}}{{\text{l}}_{\text{2}}}$
So, the number of planes of symmetry in ${\text{CC}}{{\text{l}}_{\text{4}}}$ molecule is $6$.

Thus, the correct option is (D).

Note: The hybridization of ${\text{CC}}{{\text{l}}_{\text{4}}}$ molecule is ${\text{s}}{{\text{p}}^{\text{3}}}$ hence the geometry is tetrahedral. The perfect tetrahedral always has six planes of symmetry. A perfect tetrahedral means all the valences of the central atom in tetrahedral geometry are satisfied by the same atoms. As the symmetry reduces the plane of symmetry also reduces such as if we replace the chlorine with hydrogen, geometry will be tetrahedral but the number of the plane of symmetry will not be six. The number of the plane of symmetry will reduce to three.