Question

Find the number of integral values of 'a' parameter for which the inequality $1 + \log_2(2x^2 + 2x + 7/2) \ge \log_2(\alpha x^2 + \alpha)$ has at least one root.

Answer 1

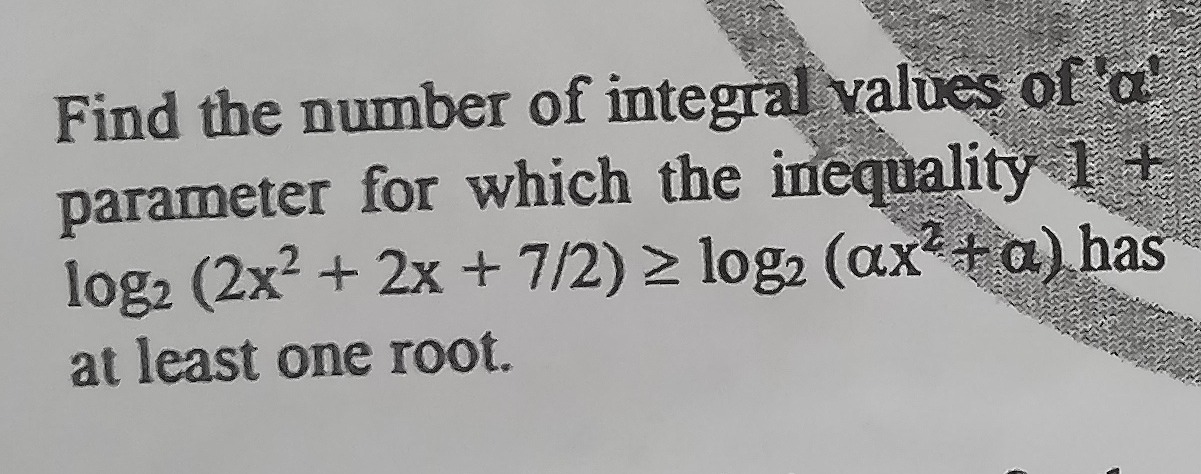
6

Answer 2

The given inequality is $1 + \log_2(2x^2 + 2x + 7/2) \ge \log_2(\alpha x^2 + \alpha)$.

Step 1: Determine the domain of the logarithmic expressions.

For $\log_2(2x^2 + 2x + 7/2)$ to be defined, $2x^2 + 2x + 7/2 > 0$. The discriminant of the quadratic $2x^2 + 2x + 7/2$ is $\Delta = (2)^2 - 4(2)(7/2) = 4 - 28 = -24$. Since the discriminant is negative ($\Delta < 0$) and the leading coefficient is positive ($2 > 0$), the quadratic $2x^2 + 2x + 7/2$ is always positive for all real values of $x$.

For $\log_2(\alpha x^2 + \alpha)$ to be defined, $\alpha x^2 + \alpha > 0$. This can be factored as $\alpha(x^2 + 1) > 0$. Since $x^2 + 1$ is always positive (in fact, $x^2 + 1 \ge 1$ for all real $x$), for the product $\alpha(x^2 + 1)$ to be positive, we must have $\alpha > 0$. This is a crucial condition for $\alpha$.

Step 2: Simplify the inequality.

The inequality can be rewritten using logarithm properties: $1 + \log_2(2x^2 + 2x + 7/2) \ge \log_2(\alpha x^2 + \alpha)$ $\log_2(2) + \log_2(2x^2 + 2x + 7/2) \ge \log_2(\alpha(x^2 + 1))$ $\log_2(2(2x^2 + 2x + 7/2)) \ge \log_2(\alpha(x^2 + 1))$ $\log_2(4x^2 + 4x + 7) \ge \log_2(\alpha x^2 + \alpha)$

Since the base of the logarithm is $2$, which is greater than $1$, the $\log_2(t)$ function is increasing. Therefore, we can remove the logarithm: $4x^2 + 4x + 7 \ge \alpha x^2 + \alpha$ Rearrange the terms to form a quadratic inequality: $(4 - \alpha)x^2 + 4x + (7 - \alpha) \ge 0$

Let $f(x) = (4 - \alpha)x^2 + 4x + (7 - \alpha)$. We need to find the integral values of $\alpha$ (with $\alpha > 0$) for which $f(x) \ge 0$ has at least one real root.

Step 3: Analyze the quadratic inequality based on the coefficient of $x^2$.

Case 1: The coefficient of $x^2$ is zero. $4 - \alpha = 0 \implies \alpha = 4$. If $\alpha = 4$, the inequality becomes: $0 \cdot x^2 + 4x + (7 - 4) \ge 0$ $4x + 3 \ge 0$ $x \ge -3/4$. This linear inequality has infinitely many solutions for $x$. Since $\alpha = 4$ satisfies the condition $\alpha > 0$, $\alpha = 4$ is a valid integral value.

Case 2: The coefficient of $x^2$ is non-zero. $4 - \alpha \ne 0$. For a quadratic $Ax^2 + Bx + C \ge 0$ to have at least one solution, we consider two sub-cases based on the sign of $A$ and the discriminant $\Delta = B^2 - 4AC$.

Subcase 2a: The parabola opens upwards. $4 - \alpha > 0 \implies \alpha < 4$. For $f(x) \ge 0$ to have at least one root, the parabola must either touch or intersect the x-axis. This means the discriminant of $f(x)$ must be non-negative ($\Delta \ge 0$). $\Delta = (4)^2 - 4(4 - \alpha)(7 - \alpha) \ge 0$ $16 - 4(28 - 4\alpha - 7\alpha + \alpha^2) \ge 0$ Divide by 4: $4 - (\alpha^2 - 11\alpha + 28) \ge 0$ $4 - \alpha^2 + 11\alpha - 28 \ge 0$ $-\alpha^2 + 11\alpha - 24 \ge 0$ Multiply by -1 and reverse the inequality sign: $\alpha^2 - 11\alpha + 24 \le 0$ Factor the quadratic: $(\alpha - 3)(\alpha - 8) \le 0$ This inequality holds when $3 \le \alpha \le 8$.

Now, combine this with the conditions for this subcase: $\alpha > 0$ (from domain) and $\alpha < 4$. The intersection of $3 \le \alpha \le 8$, $\alpha < 4$, and $\alpha > 0$ is $3 \le \alpha < 4$. The only integral value of $\alpha$ in this range is $\alpha = 3$.

Subcase 2b: The parabola opens downwards. $4 - \alpha < 0 \implies \alpha > 4$. For $f(x) \ge 0$ to have at least one root, the parabola must intersect or touch the x-axis (since it opens downwards, it will be positive between the roots if they exist). This again requires the discriminant to be non-negative ($\Delta \ge 0$). The discriminant calculation is the same as in Subcase 2a: $\Delta = (4)^2 - 4(4 - \alpha)(7 - \alpha) \ge 0 \implies 3 \le \alpha \le 8$.

Now, combine this with the conditions for this subcase: $\alpha > 0$ (from domain) and $\alpha > 4$. The intersection of $3 \le \alpha \le 8$, $\alpha > 4$, and $\alpha > 0$ is $4 < \alpha \le 8$. The integral values of $\alpha$ in this range are $\alpha = 5, 6, 7, 8$.

Step 4: Collect all valid integral values of $\alpha$. From Case 1: $\alpha = 4$. From Subcase 2a: $\alpha = 3$. From Subcase 2b: $\alpha \in \{5, 6, 7, 8\}$.

Combining all these values, the set of integral values of $\alpha$ for which the inequality has at least one root is $\{3, 4, 5, 6, 7, 8\}$. The number of integral values is 6.

The final answer is $\boxed{6}$.